Công thức Hình chữ nhật đầy đủ (bài tập có giải chi tiết)
Công thức Hình chữ nhật Toán lớp 8 sẽ giúp học sinh nắm vững công thức, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 8.
I. Lý thuyết hình chữ nhật
1. Định nghĩa
Hình chữ nhật là tứ giác có 4 góc vuông.
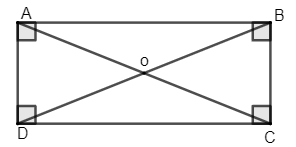
Tứ giác ABCD là hình chữ nhật.

Nhận xét:
+ Hình chữ nhật là một hình bình hành vì nó có các cặp cạnh đối song song.
ABCD là hình chữ nhật
+ Hình chữ nhật là hình thang cân vì nó có cạnh đáy song song và cặp góc ở đáy bằng nhau.
2. Tính chất.
+ Hình chữ nhật là hình bình hành và cũng là hình thang cân nên nó có tất cả các tính chất của hình bình hành và hình thang cân.
+ Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
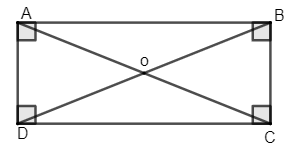
Xét hình chữ nhật ABCD ta có:

3. Dấu hiệu nhận biết
Hình chữ nhật có 4 dấu hiệu nhận biết
+ Tứ giác có ba góc vuông là hình chữ nhật.
+ Hình thang cân có một góc vuông là hình chữ nhật.
+ Hình bình hành có một góc vuông là hình chữ nhật.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
4. Định lý đường trung tuyến ứng với cạnh huyền trong tam giác vuông.
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền
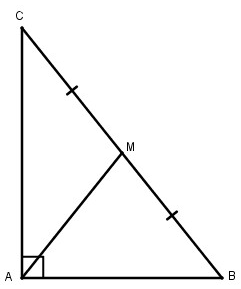
Tam giác ABC là tam giác vuông tại A
AM là đường trung tuyến của tam giác ABC ứng với cạnh huyền BC
Khi đó: 
Đinh lý đảo: Trong một tam giác có đường trung tuyến bằng nửa cạnh đáy thì tam giác đó là tam giác vuông.

II. Bài tập hình chữ nhật
Bài 1: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, AD. Tứ giác EFGH là hình gì? Vì sao?
Lời giải:
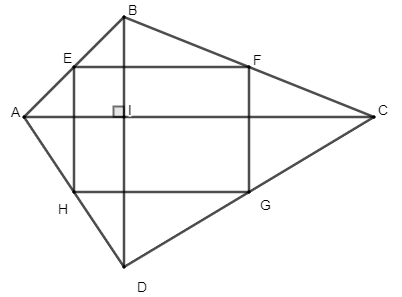
Vì E là trung điểm của AB, H là trung điểm của AD
=> EH là đường trung bình của tam giác ABD.
 (1)
(1)
Vì F là trung điểm của BC, G là trung điểm của CD
=> FG là đường trung bình của tam giác BCD
 (tính chất) (2)
(tính chất) (2)
Từ (1) và (2) => 
Xét tứ giác EFGH có
FG // EH
FG = EH
=> EFGH là hình bình hành (dấu hiệu nhận biết)
Mặt khác:

Lại có :
E là trung điểm của AB, F là trung điểm của BC.
=> EF là đường trung bình của tam giác ABC
=> EF // AC
Mà EH ⊥ AC => EH ⊥ EF

Hình bình hành EFGH có một góc vuông
=> EFGH là hình chữ nhật
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:
a) 
b) Chu vi tam giác IHK bằng nửa chu vi tam giác ABC
Lời giải:
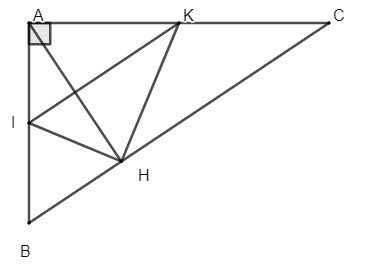
a) Vì I là trung điểm của AB nên IH = IA = IB (định lý đường trung tuyến ứng với cạnh huyển).
=> ΔIAK là tam giác cân

Vì K là trung điểm của AC nên AK = KC = HK ( định lí đường trung tuyến ứng với cạnh huyền)
=> ΔAKH là tam giác cân

Mà 
Nên 

b) Do I là trung điểm AB, K là trung điểm AC nên IK là đường trung bình của tam giác ABC

Ta có:

Chu vi tam giác HIK là:
IK + IH + KH = (BC + AB + AC)
(BC + AB + AC)
Vậy chu vi tam giác IHK bằng nửa chu vi tam giác ABC
Xem thêm các Công thức Toán lớp 8 quan trọng hay khác:
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)
