Công thức Đối xứng trục đầy đủ (bài tập có giải chi tiết)
Công thức Đối xứng trục Toán lớp 8 sẽ giúp học sinh nắm vững công thức, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 8.
I. Lý thuyết đối xứng trục
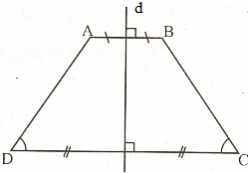
+ Hai điểm được gọi là đối xứng với nhau qua một đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
|
A đối xứng với A’ qua d khi d là trung trực của đoạn thẳng AA’
d ⊥ AA'
+ Quy ước: Một điểm nằm trên trục đối xứng thì điểm đối xứng với nó là chính nó.
+ Điểm nằm trên trục đối xứng thì cách đều hai đầu đoạn thẳng.
+ Hai hình đối xứng với nhau qua một đường thẳng là luôn có một điểm bất kỳ của hình này đối xứng với một điểm của hình kia qua đường thẳng và ngược lại.
|
+ Nếu hai đoạn thẳng, góc, tam giác đối xứng với nhau qua một đường thẳng thì bằng nhau.
+ Hình có trục đối xứng: Đường thẳng d được gọi là trục đối xứng của hình  nếu mỗi điểm đối xứng với mỗi điểm thuộc hình
nếu mỗi điểm đối xứng với mỗi điểm thuộc hình  qua đường thẳng d cũng thuộc hình
qua đường thẳng d cũng thuộc hình  .
.
|
+ Đường thẳng đi qua trung điểm hai đáy ccuar hình thang cân là trục đối xứng của hình thang cân đó.

II. Bài tập đối xứng trục.
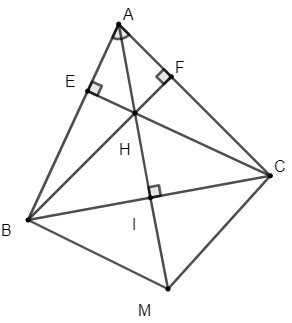
Cho tam gác ABC có  , trực tâm H. Gọi M là điểm đối xứng với H qua BC.
, trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a) Chứng minh: ΔBHC = ΔBMC
b) Tính góc 
Lời giải:
|
a) Gọi I là giao điểm của BC và MH.
Vì M đối xứng với H qua BC nên BC là trục đối xứng của MH

Xét tam giác BHC và tam giác BMC có:

=> ΔBHC = ΔBMC (c – c – c)
b) Xét tứ giác AEHF có:

Xem thêm các Công thức Toán lớp 8 quan trọng hay khác:
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)