Công thức Hình bình hành đầy đủ (bài tập có giải chi tiết)
Công thức Hình bình hành Toán lớp 8 sẽ giúp học sinh nắm vững công thức, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 8.
I. Lý thuyết hình bình hành
1. Định nghĩa:
Hình bình hành là tứ giác có các cặp cạnh đối song song.
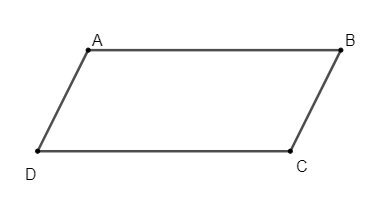
Tứ giác ABCD là hình bình hành

2. Tính chất:
Trong hình bình hành có
+ Các góc đối bằng nhau.
+ Các cạnh đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.

Xét hình bình hành ABCD có O là giáo điểm của AC và BD
Ta có:
+ AB = CD; AD = BC

+ OA = OC; OB = OD
3. Dâu hiệu nhận biết
Có 5 dấu hiệu nhận biết hình bình hành.
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có các góc đôi bằng nhau là hình bình hành.
+ Tứ giác có một cặp đôi vừa song song, vừa bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
4. Công thức tính chu vi, diện tích hình bình hành
a) Chu vi:

C = (a + b).2 (đơn vị độ dài)
Trong đó: C là chu vi
a,b là độ dài hai cạnh đáy.
b) Diện tích

S = a.h (đơn vị diện tích)
Trong đó: S là diện tích
h là chiều cao
a là độ dài đáy.

II. Bài tập hình bình hành
Bài 1: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh:
a) BE = DF và 
b) BE // DF
Lời giải:
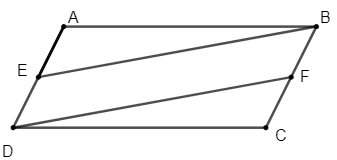
a) Vì E là trung điểm của AD, F là trung điểm của BC

Mà AD = BC do ABCD là hình bình hành.
=> AE = DE = BF = CF
Lại có do ABCD là hình bình hành:
 (tính chất)
(tính chất)
Xét tam giác ABE và tam giác CDF có:

=> ΔABE = ΔCDE (c – g – c)
=> BE = DF (hai cạnh tương ứng) và  (hai góc tương ứng)
(hai góc tương ứng)
b) Xét tứ giác EBFD có:
 (chứng minh trên)
(chứng minh trên)
Nên tứ giác EBFD là hình bình hành (dấu hiệu nhận biết).
Bài 2: Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD ở H và K. Chứng minh tứ giác AHCK là hình bình hành.
Lời giải:

Vì tứ gác ABCD là hình bình hành:

Vì AD // BC nên  (hai góc so le trong)
(hai góc so le trong)
Ta có:


Xét tam giác AHD và tam giác CKB có:

=> ΔAHD = ΔCKB (cạnh huyền góc nhọn)
=> AH = CK (hai cạnh tương ứng)
Xét tứ giác AHCK có:

=> tứ giác AHCK là hình bình hành (dấu hiệu nhận biết)
Bài 3: Cho tứ gác ABCD. Gọi M, N, P,Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD và I, K lầ trung điểm các đường chéo AC,BD. Chứng minh
a) Tứ giác MNPQ, INKQ là hình bình hành.
b) Các đường thẳng MP, NQ,IK đồng quy.
Lời giải:
|
a) Ta có:
M là trung điểm của AB; Q là trung điểm của AD
=> MQ là đường trung bình của tam giác ABD

Lại có;
N là trung điểm của BC; P là trung điểm của DC
=> PN là đường trung bình của tam giác BCD

Từ (1) và (2) => 
Xét tứ giác MNPQ có:

=> tứ giác MNPQ là hình bình hành (dấu hiệu nhận biết).
b) Vì MNPQ là hình bình hành
=> MP và NQ cắt nhau tại trung điểm mỗi đường (3)
Ta có Q là trung điểm AD; K là trung điểm của DB
=> KQ là đường trung bình của tam giác BAD

Lại có:
N là trung điểm của BC; I là trung điểm của AC
=> NI là đường trung bình của tam giác ABC

Từ (4) và (5) 
Xét tứ giác QKNI có:

=> QKNI là hình bình hành (dấu hiệu nhận biết)
=> QN và KI cắt nhau tại trung điểm mỗi đường (6)
Từ (3) và (6) => NQ, MP, KI đồng quy
Xem thêm các Công thức Toán lớp 8 quan trọng hay khác:
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

