Cho hình thang vuông ABCD

Trang trước Trang sau

Bài 4.65 trang 70 sách bài tập Toán lớp 10 Tập 1: Cho hình thang vuông ABCD có $\hat{D A B} = \hat{A B C} = 90 °,$ BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm của AB.

a) Hãy biểu thị các vectơ $\vec{C M}, \vec{C M}$ theo hai vectơ $\vec{A B}$ và $\vec{A D} .$

b) Gọi N là trung điểm CD, G là trọng tâm tam giác MCD, và I là điểm thuộc cạnh CD sao cho 9IC = 5ID. Chứng minh rằng A, G, I thẳng hàng.

c) Tính độ dài các đoạn thẳng AI và BI.

Lời giải:

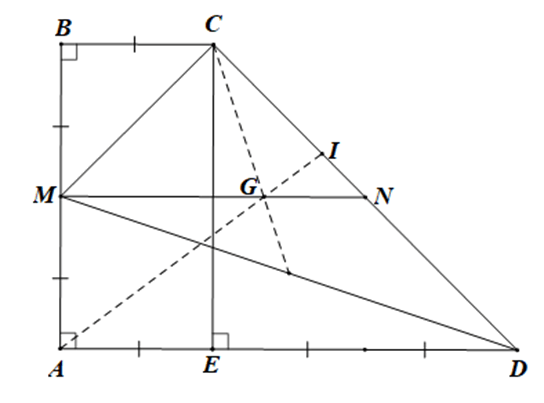
a) Vì M là trung điểm của AB nên $\vec{B M} = \frac{1}{2} \vec{B A} = - \frac{1}{2} \vec{A B}$

Gọi E là hình chiếu của C trên AD. Khi đó $\hat{C E A} = 90 °$

Tứ giác ABCE có $\hat{D A B} = \hat{A B C} = \hat{C E A} = 90 °$ nên là hình chữ nhật

$\Rightarrow$ EA = CB = 1

Mà AD = 3 do đó AE = $\frac{1}{3}$ AD

$\Rightarrow \vec{E A} = \frac{1}{3} \vec{D A} = - \frac{1}{3} \vec{A D}$

Mà $\vec{C B} = \vec{E A}$ (do ABCE là hình chữ nhật)

$\Rightarrow \vec{C B} = - \frac{1}{3} \vec{A D}$

$\Rightarrow \vec{C M} = \vec{C B} + \vec{B M} = - \frac{1}{3} \vec{A D} - \frac{1}{2} \vec{A B}$

• Ta có: $\vec{C D} = \vec{C E} + \vec{E D}$

Mà $\vec{C E} = \vec{B A}$ (do ABCE là hình chữ nhật)

Và $\vec{E D} = \frac{2}{3} \vec{A D}$

$\Rightarrow \vec{C D} = \vec{B A} + \frac{2}{3} \vec{A D} = - \vec{A B} + \frac{2}{3} \vec{A D}$

Vậy $\vec{C M} = - \frac{1}{3} \vec{A D} - \frac{1}{2} \vec{A B}$ và $\vec{C D} = - \vec{A B} + \frac{2}{3} \vec{A D} .$

b) Vì G là trọng tâm của tam giác MCD nên ta có:

$\vec{A M} + \vec{A C} + \vec{A D} = 3 \vec{A G}$

ABCD là hình chữ nhật nên cũng là hình bình hành

Do đó $\vec{A C} = \vec{A B} + \vec{A E}$

$\Rightarrow 3 \vec{A G} = \vec{A M} + (\vec{A B} + \vec{A E}) + \vec{A D}$

$= \frac{1}{2} \vec{A B} + \vec{A B} + \frac{1}{3} \vec{A D} + \vec{A D}$ (do $\vec{A E} = \frac{1}{3} \vec{A D}$ )

$= \frac{3}{2} \vec{A B} + \frac{4}{3} \vec{A D}$

Vì I thuộc cạnh CD nên hai vectơ $\vec{I C}$ và $\vec{I D}$ ngược hướng nhau

Lại có 9IC = 5ID nên $9 \vec{I C} = - 5 \vec{I D}$ hay $\vec{I C} = - \frac{5}{9} \vec{I D}$

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:

$\vec{A C} - (- \frac{5}{9}) \vec{A D} = (1 - (- \frac{5}{9})) \vec{A I}$

$\Rightarrow \vec{A C} + \frac{5}{9} \vec{A D} = (1 + \frac{5}{9}) \vec{A I}$

$\Rightarrow \vec{A C} + \frac{5}{9} \vec{A D} = \frac{14}{9} \vec{A I}$

$\Rightarrow 14 \vec{A I} = 9 \vec{A C} + 5 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 9 (\vec{A B} + \vec{A E}) + 5 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 9 \vec{A B} + 9 \vec{A E} + 5 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 9 \vec{A B} + 9. \frac{1}{3} \vec{A D} + 5 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 9 \vec{A B} + 8 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 6 (\frac{3}{2} \vec{A B} + \frac{4}{3} \vec{A D})$

$\Rightarrow 14 \vec{A I} = 6.3 \vec{A G}$ (do $3 \vec{A G} = \frac{3}{2} \vec{A B} + \frac{4}{3} \vec{A D}$ )

$\Rightarrow 14 \vec{A I} = 18 \vec{A G}$

$\Rightarrow \vec{A I} = \frac{9}{7} \vec{A G}$

Do đó hai vectơ $\vec{A I}$ và $\vec{A G}$ cùng phương

Suy ra ba điểm A, I, G thẳng hàng.

c) • Theo câu a ta có $14 \vec{A I} = 9 \vec{A B} + 8 \vec{A D}$

$\Rightarrow {(14 \vec{A I})}^{2} = {(9 \vec{A B} + 8 \vec{A D})}^{2}$

$\Rightarrow 196 A I^{2} = 81 A B^{2} + 2. (9 \vec{A B}) . (8 \vec{A D}) + 64 A D^{2}$

Mà AB ⊥ AD nên $\vec{A B} . \vec{A D} = 0$

Do đó ta có: 196AI² = 81AB² + 64AD²

$\Rightarrow$ 196AI² = 81.2² + 64.3² = 900

$\Rightarrow$ AI² = $\frac{225}{49}$

$\Rightarrow$ AI = $\frac{15}{7} .$

• Ta có: $14 \vec{A I} = 9 \vec{A B} + 8 \vec{A D} \Rightarrow \vec{A I} = \frac{9}{14} \vec{A B} + \frac{4}{7} \vec{A D}$

$\Rightarrow$ $\vec{B I} = \vec{A I} - \vec{A B} = \frac{9}{14} \vec{A B} + \frac{4}{7} \vec{A D} - \vec{A B}$

$\Rightarrow \vec{B I} = - \frac{5}{14} \vec{A B} + \frac{4}{7} \vec{A D}$

$\Rightarrow {(\vec{B I})}^{2} = {(- \frac{5}{14} \vec{A B} + \frac{4}{7} \vec{A D})}^{2}$

$\Rightarrow B I^{2} = \frac{25}{196} A B^{2} - 2. \frac{5}{14} \vec{A B} . \frac{4}{7} \vec{A D} + \frac{16}{49} A D^{2}$

$\Rightarrow B I^{2} = \frac{25}{196} A B^{2} + \frac{16}{49} A D^{2}$ (do $\vec{A B} . \vec{A D} = 0$ )

$\Rightarrow B I^{2} = \frac{25}{196} {.2}^{2} + \frac{16}{49} {.3}^{2} = \frac{169}{49}$

$\Rightarrow$ BI = $\frac{13}{7} .$

Vậy AI = $\frac{15}{7}$ và BI = $\frac{13}{7} .$

Xem thêm các bài giải sách bài tập Toán lớp 10 sách Kết nối tri thức hay, chi tiết khác:

Trang trước Trang sau

Giải bài tập lớp 10 Kết nối tri thức khác