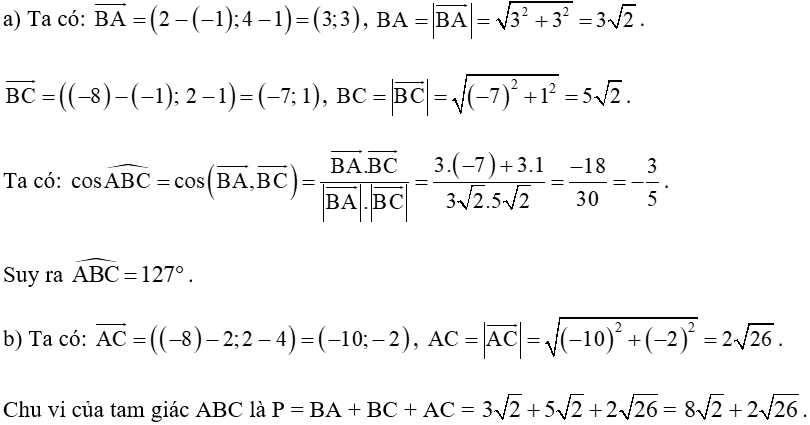Bài 4 trang 72 Toán 10 Tập 2 Cánh diều
Bài 4 trang 72 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2; 4); B(– 1; 1); C(– 8; 2).
a) Tính số đo góc ABC (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
b) Tính chu vi của tam giác ABC.
c) Tìm tọa độ điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM.
Lời giải:
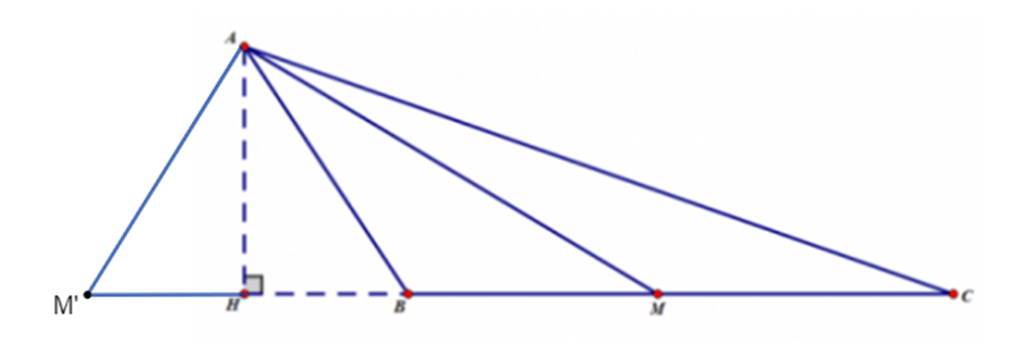
c)
Vì nên tam giác ABC tù.
Kẻ đường cao AH của tam giác ABC, M thuộc đường thẳng BC nên đường cao của tam giác ABM cũng là AH.
Khi đó: SABC = AH . BC và SABM = AH . BM.
Theo bài ra ta có diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM nên SABC = 2SABM.
Do đó: AH . BC = 2 . AH . BM ⇔ BC = 2BM hay BM = BC.
Suy ra M là trung điểm của BC hoặc M là điểm đối xứng với trung điểm của BC qua B.
Trường hợp 1: M là trung điểm của BC nên tọa độ của M là , .
Vậy .
Trường hợp 2: M là điểm đối xứng với trung điểm BC qua B.
Khi đó điểm cần tìm là M', với B là trung điểm của MM'.
Ta có: xM' = 2xB – xM = 2 . (– 1) – , yM' = 2 . 1 – .
Vậy .
Lời giải Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ hay, chi tiết khác:
Câu hỏi khởi động trang 67 Toán lớp 10 Tập 2: Trên màn hình ra đa của đài kiểm soát không lưu ....
Hoạt động 1 trang 67 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy (Hình 18), cho hai vectơ ....
Bài 1 trang 72 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho , , ....
Bài 5 trang 72 Toán lớp 10 Tập 2: Cho ba điểm A(1; 1) ; B(4; 3) và C (6; – 2). ....
Bài 6 trang 72 Toán lớp 10 Tập 2: Chứng minh khẳng định sau ....
Bài 7 trang 72 Toán lớp 10 Tập 2: Một vật đồng thời bị ba lực tác động: lực tác động thứ nhất ....
Các bài học để học tốt Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ:
Giải SBT Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ
Lý thuyết Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ
Trắc nghiệm Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Cánh diều
- Giải Chuyên đề học tập Toán 10 Cánh diều
- Giải SBT Toán 10 Cánh diều
- Giải lớp 10 Cánh diều (các môn học)
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Soạn văn 10 (hay nhất) - Cánh diều
- Soạn văn 10 (ngắn nhất) - Cánh diều
- Soạn văn 10 (siêu ngắn) - Cánh diều
- Giải sgk Toán 10 - Cánh diều
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - Cánh diều
- Giải sgk Hóa học 10 - Cánh diều
- Giải sgk Sinh học 10 - Cánh diều
- Giải sgk Địa lí 10 - Cánh diều
- Giải sgk Lịch sử 10 - Cánh diều
- Giải sgk Kinh tế và Pháp luật 10 - Cánh diều
- Giải sgk Tin học 10 - Cánh diều
- Giải sgk Công nghệ 10 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 10 - Cánh diều
- Giải sgk Giáo dục quốc phòng 10 - Cánh diều