Top 50 Đề thi Toán 6 Giữa kì 1 năm 2025 (cấu trúc mới, có đáp án)

Bộ 50 Đề thi Giữa kì 1 Toán 6 năm 2025 có đáp án theo cấu trúc mới sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh ôn luyện để đạt điểm cao trong các bài thi Toán 6 Giữa học kì 1.

Xem thử Đề thi GK1 Toán 6 KNTT Xem thử Đề thi GK1 Toán 6 CTST Xem thử Đề thi GK1 Toán 6 CD

Chỉ từ 150k mua trọn bộ Đề thi Toán 6 Giữa kì 1 (mỗi bộ sách) theo cấu trúc mới bản word có lời giải chi tiết:

B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

Đề thi Giữa kì 1 Toán 6 theo bộ sách

Đề thi Toán 6 Giữa kì 1 theo tỉnh (trên cả nước)

- Đề thi Giữa kì 1 Toán 6 Hà Nội

- Đề thi Giữa kì 1 Toán 6 TP Hồ Chí Minh

Đề thi Giữa kì 1 Toán 6 năm 2025 phòng GD&ĐT Quận 3 (Tp. HCM)

Đề thi Giữa kì 1 Toán 6 năm 2025 phòng GD&ĐT Thủ Đức (Tp. HCM)

Đề thi Giữa kì 1 Toán 6 năm 2025 phòng GD&ĐT Hóc Môn (Tp. HCM)

- Đề thi Giữa kì 1 Toán 6 Nam Định

- Đề thi Giữa kì 1 Toán 6 Bà Rịa - Vũng Tàu

Đề thi Giữa kì 1 Toán 6 năm 2025 trường THCS Nguyễn Huệ (Bà Rịa - Vũng Tàu)

- Đề thi Giữa kì 1 Toán 6 Hải Phòng

- Đề thi Giữa kì 1 Toán 6 Bắc Giang

- Đề thi Giữa kì 1 Toán 6 Hải Dương

Đề thi Giữa kì 1 Toán 6 năm 2025 trường THCS Tân Bình (Hải Dương)

- Đề thi Giữa kì 1 Toán 6 Bắc Ninh

Đề thi Giữa kì 1 Toán 6 năm 2025 sở GD&ĐT Bắc Ninh

- Đề thi Giữa kì 1 Toán 6 Quảng Ninh

Đề thi Giữa kì 1 Toán 6 năm 2025 trường THCS thị trấn Cái Rồng (Quảng Ninh)

- Đề thi Giữa kì 1 Toán 6 Vĩnh Phúc

Đề thi Giữa kì 1 Toán 6 năm 2025 sở GD&ĐT Lập Thạch (Vĩnh Phúc)

- Đề thi Giữa kì 1 Toán 6 Quảng Nam

Đề thi Giữa kì 1 Toán 6 năm 2025 trường THCS Nguyễn Du (Quảng Nam)

- Đề thi Giữa kì 1 Toán 6 Hà Tĩnh

Đề thi Giữa kì 1 Toán 6 năm 2025 trường THCS Phúc Lộc (Hà Tĩnh)

- Đề thi Giữa kì 1 Toán 6 Tây Ninh

Đề thi Giữa kì 1 Toán 6 năm 2025 trường THCS Biên Giới (Tây Ninh)

Xem thử Đề thi GK1 Toán 6 KNTT Xem thử Đề thi GK1 Toán 6 CTST Xem thử Đề thi GK1 Toán 6 CD

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Bài thi môn: Toán 6

Năm 2025

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

A. TRẮC NGHIỆM (7,0 điểm)

Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)

Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.

Câu 1. Biểu diễn tập hợp $H = \{2; 4; 6; 8; 10\}$ bằng cách chỉ ra tính chất đặc trưng của nó là

A. $H = \{x \in ℕ | x$ là số chẵn và $x \leq 10\} .$

B. $H = \{x \in ℕ | x$ là số chẵn và $x < 10\} .$

C. $H = \{x \in ℕ * | x$ là số chẵn và $x \leq 10\} .$

D. $H = \{x \in ℕ * | x < 10\} .$

Câu 2. Khi thêm I vào phía trước số La Mã XX, phát biểu đúng là

A. Số ban đầu có giá trị giảm xuống 1 đơn vị.

B. Số ban đầu có giá trị tăng thêm 1 đơn vị.

C. Số mới có giá trị trong hệ thập phân là 21.

D. Không thể thêm vào như thế vì trái với quy tắc viết số La Mã.

Câu 3. Biểu thức nào sau đây sử dụng đúng dấu ngoặc?

A. $200 : (2 \cdot [20 - \{10 + 5\}]) .$

B. $200 : \{2 \cdot (20 - [10 + 5])\} .$

C. $200 : \{2 \cdot [20 - (10 + 5)]\} .$

D. $200 : [2 \cdot \{20 - (10 + 5)\}] .$

Câu 4. Kết quả của phép tính $a^{m} : a^{n}$ là

A. $a^{m : n} .$

B. $a^{m \cdot n} .$

C. $a^{m - n} .$

D. ${(a^{m})}^{n} .$

Câu 5. Kết quả của phép tính $2^{15} : (2^{6} \cdot 32)$ viết dưới dạng lũy thừa của cơ số 4 có số mũ là

A. 1.

B. 2.

C. 3.

D. 4.

Câu 6. Những số nào sau đây là ước của 36?

A. 2; 3; và 6.

B. 0; 1 và 6.

C. 12; 18 và 24.

D. 36; 72 và 108.

Câu 7. Khẳng định nào sau đây là sai?

A. Một số chia hết cho 3 thì số đó chia hết cho 9.

B. Một số chia hết cho 9 thì số đó chia hết cho 3.

C. Một số chia hết cho 10 thì số đó chia hết cho 5.

D. Một số chia hết cho 45 thì số đó chia hết cho 9.

Câu 8. Bạn An có ngày sinh là số nguyên tố lớn nhất nhỏ hơn 20, tháng sinh của bạn là số nguyên tố nhỏ nhất. Vậy bạn An có ngày và tháng sinh là bao nhiêu?

A. Ngày 19 tháng 3

B. Ngày 19 tháng 2

C. Ngày 7 tháng 2

D. Ngày 7 tháng 3

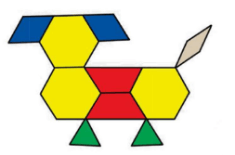
Câu 9. Cho hình vẽ sau:

10 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 (có đáp án)

Trong hình vẽ trên có:

A. 2 hình thang, 3 hình lục giác đều, 3 hình tam giác đều.

B. 2 hình thoi, 3 hình lục giác đều, 2 hình thang cân.

C. 3 hình lục giác đều, 2 hình thang cân, 2 hình tam giác đều.

D. 2 hình tam giác đều, 1 hình lục giác đều, 4 hình thoi.

Câu 10. Hình nào trong các hình sau có 2 cạnh đối song song và 2 đường chéo bằng nhau?

A. Hình bình hành.

B. Hình thang cân.

C. Hình thoi.

D. Hình tam giác đều.

Câu 11. Khẳng định nào sau đây là sai?

A. Hình chữ nhật và hình thoi có các cặp cạnh đối song song với nhau.

B. Hình lục giác đều có ba đường chéo chính bằng nhau.

C. Hình bình hành có hai cạnh đối bằng nhau.

D. Hình thoi có hai đường chéo bằng nhau.

Câu 12. Một hình bình hành có độ dài cạnh đáy là và diện tích là thì có chiều cao tương ứng với cạnh đáy đã cho là

A. $h = \frac{S}{a} .$

B. $h = \frac{S}{2 a} .$

C. $h = \frac{2 S}{a} .$

D. Cả A, B, C đều sai.

Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)

Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Câu 13. Cho số tự nhiên có hai chữ số.

a) Trong các số đã cho, có 10 số chia hết cho cả 2 và 5.

b) Trong các số đã cho, có 29 số chia hết cho 3.

c) Trong các số đã cho, có 5 số là chia hết cho cả 2 và 9.

d) Tổng của các số là bội của 18 khi phân tích thành nhân tử được thừa số có số mũ cao nhất là 3.

Câu 14. Cho hình vuông ABCD có cạnh bằng 4 cm. Khi đó

a) AB = BC = CD = DA = 4 cm.

b) AB và BD song song với nhau.

c) Mỗi góc ở các đỉnh của hình vuông bằng nhau và bằng 60°.

d) Vẽ cạnh AB = 4 cm. Dùng thước eke vẽ các đường vuông góc với AB tại A, B, sau đó lần lượt lấy các điểm D, C trên các đường đó sao cho AD = BC = 4 cm. Nối C với D ta được hình vuông ABCD có cạnh 4 cm như đã cho.

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)

Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 15. Có bao nhiêu số tự nhiên m sao cho 2125 < m < 2154 và chia hết cho 9?

Câu 16. Có bao nhiêu số tự nhiên n thỏa mãn 25 < 3ⁿ < 260?

Câu 17. Một trường Trung học cơ sở có 997 học sinh tham dự lễ tổng kết cuối năm. Ban tổ chức đã chuẩn bị những chiếc ghế băng 5 chỗ ngồi. Phải có ít nhất bao nhiêu ghế băng như vậy để tất cả học sinh đều có chỗ ngồi?

Câu 18. Một hình thoi có diện tích là 220 cm² và độ dài đường chéo lớn là 22 cm. Tính độ dài đường chéo nhỏ của hình thoi đó (đơn vị: cm).

B. TỰ LUẬN (3,0 điểm)

Bài 1. (1,5 điểm)

1) Thực hiện phép tính (tính hợp lí nếu có thể):

a) $39 - 125 : [(5^{11} \cdot 16 + 9 \cdot 5^{11}) : 5^{12}] .$

b) $57 \cdot 34 + 100 \cdot 43 + 57 \cdot 66.$

2) Tìm $x,$ biết: $121 + (5 x - 21) : 4 = 127.$

Bài 2. (1,0 điểm) Một khu đất hình thang cân ABCD có độ dài các cạnh đáy lần lượt là 30 m và 36 m và chiều cao là 25 m. Trong khu đất đó, người ta đào một cái ao hình vuông EFGH như hình vẽ, phần đất còn lại trồng hoa.

10 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 (có đáp án)

a) Tính diện tích phần đất trồng hoa, biết EF = 15 m.

b) Để giữ bờ, người ta trồng cây xung quanh bờ ao, biết rằng cây đầu tiên trồng ở điểm E và cứ 3 m thì người ta trồng một cây. Hỏi quanh bờ ao, trồng được bao nhiêu cây?

Bài 3. (0,5 điểm) Cho biểu thức $A = 2 + 21^{23} + 25^{125} .$ Chứng minh rằng A là hợp số.

-----HẾT-----

10 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 (có đáp án)

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Bài thi môn: Toán 6

Năm 2025

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

I. Trắc nghiệm (2 điểm)

Câu 1. Không làm phép tính hãy cho biết tổng nào sau đây chia hết cho 5?

A. 80 + 1 945 + 15.

B. 1 930 + 100 + 21.

C. 34 + 105 + 20.

D. 1 025 + 2 125 + 46.

Câu 2. Tính 14 + 2.8².

A. 142;

B. 143;

C. 144;

D. 145

Câu 3. Phát biểu dưới đây là sai?

A. 6 là ước của 12.

B. 35 + 14 chia hết cho 7.

C. 121 là bội của 12.

D. 219. 26 + 13 chia hết cho 13.

Câu 4: Số La Mã biểu diễn số 29 là?

A. XIX;

B. XXIX;

C. XXXI;

D. XXVIV.

II. Tự luận (8 điểm)

Bài 1. (2 điểm) Thực hiện phép tính:

a) 120 + [55 – (11 – 3.2)²] + 2³;

b) 2³.3 - (1¹⁰ + 15) : 4²;

c) 21.[(1 245 + 987):2³ – 15.12] + 21;

d) 321 – 21.[(2.3³ + 4⁴:32) – 52].

Bài 2. (2 điểm) Tìm giá trị của x thỏa mãn:

a) 3(5x – 15) – 52 = 68;

b) {2³ + [1 + (3 – 1)²]}:x = 13;

c) 32 < 2^x ≤ 512;

d) Thay x trong số Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 có đáp án (15 đề) bằng chữ số thích hợp để số đó chia hết cho 9.

Bài 3. (2 điểm) Trong một buổi tập đồng diễn thể dục có khoảng 400 đến 500 người tham gia. Thầy tổng phụ trách cho xếp thành hàng 5, hàng 6 và hàng 8 thì đều thừa một người. Hỏi có chính xác bao nhiêu người dự buổi tập đồng diễn thể dục.

Bài 4. (1 điểm) Trong một phép chia, số bị chia là 89, số dư là 12. Tìm số chia và thương.

Bài 5. (1 điểm) Gọi A = n² + n + 1 (với n ∈ N). Chứng tỏ rằng A không chia hết cho 4.

I. Trắc nghiệm (2 điểm)

Câu 1.

Ta có:

+) Vì 80 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 có đáp án (15 đề) 5; 1 945 5; 15 5 nên 80 + 1 945 + 15 5. Do đó A đúng.

+) Vì 1 930 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 có đáp án (15 đề) 5; 100 5 và 21 5 nên 1 930 + 100 + 21 không chia hết cho 5. Do đó B sai.

+) Vì 105 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 có đáp án (15 đề) 5; 20 5 và 34 5 nên 34 + 105 + 20 không chia hết cho 5. Do đó C sai.

+) Vì 1 025 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 có đáp án (15 đề) 5; 2 125 5 và 46 5 nên 1 025 + 2 125 + 46 không chia hết cho 5. Do đó D sai.

Chọn A.

Câu 2.

14 + 2.8² = 14 + 2.64 = 14 + 128 = 142.

Chọn A.

Câu 3.

Ta có 12 chia hết cho 6 nên 6 là ước của 12. Do đó A đúng.

Vì 35 chia hết cho 7 và 14 chia hết cho 7 nên 35 + 14 chia hết cho 7. Do đó B đúng.

121 không chia hết cho 12 nên 121 không là bội của 12. Do đó C sai.

Ta có 219.26 = 219.13.2 chia hết cho 13, 13 cũng chia hết cho 13 nên 219.26 + 13 chia hết cho 13. Do đó D đúng.

Chọn C.

Câu 4.

Số La Mã biểu diễn cho số 29 là: XXIX.

Chọn B.

II. Tự luận (8 điểm)

Bài 1.

a) 120 + [55 – (11 – 3.2)²] + 2³

= 120 + [55 – (11 – 6)²] + 8

= 120 + [55 – 5²] + 8

= 120 + [55 – 25] + 8

= 120 + 30 + 8

= 150 + 8

= 158.

b) 2³.3 - (1¹⁰ + 15) : 4²

= 8.3 - (1 + 15) : 16

= 24 - 16 : 16

= 24 - 1

= 23.

c) 21.[(1 245 + 987):2³ – 15.12] + 21

= 21.[2 232:8 – 180] + 21

= 21.[279 – 180] + 21

= 21.99 + 21

= 21(99 + 1)

= 21.100

= 2 100.

d) 321 – 21.[(2.3³ + 4⁴:32) – 52].

= 321 – 21[2.27 + 64:32) – 52]

= 321 – 21[54 + 2 – 52]

= 321 – 21.4

= 321 – 84

= 237.

Bài 2.

a) 3(5x – 15) – 52 = 68

3(5x – 15) = 68 + 52

3(5x – 15) = 120

5x – 15 = 120:3

5x – 15 = 40

5x = 40 + 15

5x = 55

x = 55:5

x = 11.

Vậy x = 11.

b) {2³ + [1 + (3 – 1)²]}:x = 13

{8 + [1 + 2²]}:x = 13

{8 + [1 + 4]}:x = 13

{8 + 5}:x = 13

13:x = 13

x = 13:13

x = 1.

Vậy x = 1.

c) Ta có: 32 < 2^x ≤ 512

Mà 32 = 2.2.2.2.2 = 2⁵; 512 = 2.2.2.2.2.2.2.2.2 = 2⁹.

Nghĩa là 2⁵ < 2^x ≤ 2⁹.

Khi đó: 5 < x ≤ 9, mà x là số tự nhiên nên x ∈ {6; 7; 8; 9}.

Vậy x ∈ {6; 7; 8; 9}.

d) Ta có 2 + 3 + x + 5 = 10 + x.

Để số đã cho chia hết cho 9 thì 10 + x phải chia hết cho 9.

Nên x thuộc {8; 17; 26; …}.

Mà x là chữ số nên x = 8.

Vậy x = 8.

Bài 3.

Gọi số người tham gia buổi tập đồng diễn thể dục là x (x ∈ N, 400 < x < 500).

Do số người tham gia xếp thàng hàng 5, hàng 6 và hàng 8 đều thừa một người nên ta có:

x – 1 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 có đáp án (15 đề) 5

x – 1 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 có đáp án (15 đề) 6

x – 1 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2025 có đáp án (15 đề) 8

nên x – 1 ∈ BC(5, 6, 8).

Ta có 5 = 5, 6 = 2.3, 8 = 2³.

Khi đó: BCNN(5, 6, 8) = 2³.3.5 = 8.3.5 = 120.

Suy ra BC(5, 6, 8) = B(120) = {0; 120; 240; 360; 480; 600; …}.

Do đó x – 1 ∈ {0; 120; 240; 360; 480; 600; …}.

Hay x ∈ {1; 121; 241; 361; 481; 601; …}.

Mà 400 < x < 500 nên x = 481.

Bài 4.

Gọi số chia và thương lần lượt là b và q (b; q ∈ N, b ≠0).

Như vậy 89 : b = q (dư 12) và b > 12 (số chia lớn hơn số dư).

Từ đó 89 = bq + 12. Suy ra bq = 89 – 12 = 77 = 7 . 11 = 77 . 1

Mà b > 12 nên b = 77 và q = 1.

Do đó 89 : 77 = 1 (dư 12).

Vậy số chia bằng 77, thương bằng 1.

Bài 5.

Ta có: A = n² + n + 1 = n(n+1)+1

Vì n ∈ N nên n + 1 ∈ N.

Nếu n là số chẵn thì n(n + 1) chia hết cho 2.

Nếu n là số lẻ thì n + 1 là số chẵn nên n(n + 1) chia hết cho 2.

Do đó n(n + 1) chia hết cho 2 với mọi số tự nhiên n.

Mà 1 không chia hết cho 2 nên n(n+1) + 1 không chia hết cho 2.

Suy ra n(n + 1) + 1 không chia hết cho 2 với mọi số tự nhiên n.

Vậy A không chia hết cho 4 với mọi số tự nhiên n.

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Cánh diều

Bài thi môn: Toán 6

Năm 2025

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

A. Đề bài

I. Phần trắc nghiệm (4 điểm)

Câu 1: Tập hợp nào dưới đây có 5 phần tử?

A. A = {x ∈ N*| x > 3}

B. B = {x ∈ N| x < 6}

C. C = {x ∈ N | x ≤ 4}

D. D = {x ∈ N^* | 4 < x ≤ 8}

Câu 2: Cho tập hợp M các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3. Phần tử nào dưới đây không thuộc tập hợp M?

A. 13 B. 23 C. 33 D. 43

Câu 3: Số 1 080 chia hết cho bao nhiêu số trong các số sau đây: 2, 3, 4, 5, 6, 8, 9, 12, 24, 25?

A. 10 số B. 9 số C. 8 số D. 7 số

Câu 4: Hằng gấp được 97 ngôi sao và xếp vào các hộp, mỗi hộp 8 ngôi sao. Số ngôi sao còn thừa không xếp vào hộp là:

A. 5 ngôi sao

B. 1 ngôi sao

C. 6 ngôi sao

D. 2 ngôi sao

Câu 5: Phân tích số 154 ra thừa số nguyên tố được:

A. 154 = 2 . 7 . 11

B. 154 = 1 . 5 . 4

C. 154 = 2² . 3 . 5

D. 154 = 2 . 7 . 13

Câu 6: Hình nào dưới đây là hình vẽ chỉ tam giác đều?

B. Đề thi Giữa kì 1 Toán 6 có đáp án (15 đề) | Cánh diều

C. Đề thi Giữa kì 1 Toán 6 có đáp án (15 đề) | Cánh diều

D. Đề thi Giữa kì 1 Toán 6 có đáp án (15 đề) | Cánh diều

Câu 7: Hai đường chéo hình thoi có độ dài lần lượt bằng 16 cm và 12 cm. Diện tích của hình thoi là:

A. 90 cm² B. 96 cm² C. 108 cm² D. 120 cm²

Câu 8: Chọn câu sai trong các câu dưới đây?

Cho hình vẽ

Đề thi Giữa kì 1 Toán 6 có đáp án (15 đề) | Cánh diều

Lục giác đều ABCDEG là hình có:

A. Các góc ở các đỉnh A, B, C, D, E, G, O bằng nhau.

B. Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.

C. Ba đường chéo chính cắt nhau tại điểm O.

D. Ba đường chéo chính bằng nhau: AD = BE = CG.

II. Phần tự luận (6 điểm)

Bài 1 (2 điểm):

1) Thực hiện các phép tính:

a) 30 . 75 + 25 . 30 – 150;

b) 160 – (4 . 5² – 3 . 2³);

c) [36 . 4 – 4 . (82 – 7 . 11)²] : 4 – 2022⁰.

2) Tìm BCNN của các số 28, 54.

Bài 2 (1,5 điểm): Tính diện tích của hình H gồm hình bình hành ABCD và hình chữ nhật DCNM, biết hình chữ nhật DCNM có chu vi bằng 180 cm và chiều dài MN gấp 4 lần chiều rộng CN.

Đề thi Giữa kì 1 Toán 6 có đáp án (15 đề) | Cánh diều

Bài 3 (2 điểm):Một đội y tế gồm 48 bác sĩ và 108 y tá. Hỏi có thể chia đội y tế thành nhiều nhất bao nhiêu tổ để số bác sĩ và y tá được chia đều vào các tổ?

Bài 4 (0,5 điểm):Chứng tỏ A chia hết cho 6 với A = 2 + 2² + 2³ + 2⁴ + … + 2¹⁰⁰.

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Chân trời sáng tạo

Bài thi môn: Toán 6

Năm 2025

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

I. Phần trắc nghiệm

Câu 1: Viết tập hợp sau A = {x∈ N | 8 ≤ x ≤ 12} bằng cách liệt kê các phần tử:

A) A = {8; 9; 10; 11; 12}

B) A = {9; 10; 11; 12}

C) A = {9; 10; 11}

D) A = {9; 10; 11; 12}

Câu 2: Số tự nhiên chia cho 10 dư 5 có dạng

A) 5k + 10 (với k ∈ N)

B) 5k -10 (với k ∈ N)

C) 10k + 3 (với k ∈ N)

D) 10k + 5 (với k ∈ N)

Câu 3: Phân tích số 300 ra thừa số nguyên tố

A) 2³.3.5²

B) 2².3.5²

C) 2.3².5²

D) 2³.3.5

Câu 4: Kết quả của phép tính: 250 - 5² - (3² +12):3

A) 218

B) 268

C) 232

D) 240

Câu 5: Trong các khẳng định sau, khẳng định nào sai

A) Số đối của số -6 là số 6.

B) Số đối của số 0 là số 0.

C) Số -5 nằm bên trái số -4 nên ta nói -5 lớn hơn – 4.

D) Số 0 không phải số nguyên âm cũng không phải số nguyên dương.

Câu 6: Trong các dãy số dưới đây, dãy nào chỉ toàn là số nguyên tố.

A) 1; 3; 5; 7

B) 2; 3; 5; 7

C) 1; 2; 3; 5; 7

D) 3; 5; 7; 9

Câu 7: Cho các số nguyên sau: 0; -3; 2; 5; -4; 4; 6. Sắp xếp các số nguyên đã cho theo thứ tự tăng dần

A) -3; -4; 0; 2; 4; 5; 6

B) 0; -3; -4; 2; 4; 5; 6

C) 6; 5; 4; 2; 0; -3; -4

D) -4; -3; 0; 2; 4; 5; 6

Câu 8: Tập hợp A = {a ∈ Z | -5 < a < 2}

A) 5

B) 7

C) 6

D) 8

Câu 9: Tìm số x ∈ Z thỏa mãn: 2x + 35 = 17

A) 12

B) 9

C) 26

D) -9

Câu 10: Kết quả của phép tính: 2³ - 2.(-3) + 5²

A) 39

B) 25

C) 27

D) 14

II. Tự luận

Bài 1: Thực hiện phép tính

a) (4 + 32 + 6) + (10 – 32 – 2)

b) (56.35 + 56.18):53

c) 12:{400:[500 – (125 + 25.7)]}

d) 303 – 3.{[655 – (18:2 + 1). +5]}: 10⁰

Bài 2: Tìm x ∈ Z biết:

a) 2² + (x + 3) = 5²

b) 125 – 5(4 + x) = 15

c) (15 + x):3 = 3¹⁵ : 3¹²

d) 2^x+1- 2^x = 32

Bài 3: Bạn Vinh có 48 viên bi đỏ, 30 viên bi xanh, 66 viên bi vàng. Vinh muốn chia đều số bi vào các túi sao cho mỗi túi đều có cả ba loại bi. Hỏi Vinh có thể chia nhiều nhất bao nhiêu túi. Khi đó mỗi túi có bao nhiêu viên bi mỗi loại.

Bài 4: Tìm các số tự nhiên x; y biết 2xy + x + 2y = 13

................................

Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 6 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử Đề thi GK1 Toán 6 KNTT Xem thử Đề thi GK1 Toán 6 CTST Xem thử Đề thi GK1 Toán 6 CD

Xem thêm đề thi Toán 6 có đáp án, chọn lọc hay khác:

Xem thêm đề thi lớp 6 các môn học có đáp án hay khác:

Tài liệu giáo án lớp 6 các môn học chuẩn khác:

Mục lục Đề thi Toán 6 theo chương và học kì:

Trang trước

Trang sau

Đề thi, giáo án lớp 6 các môn học