Các bài toán về các tập hợp số và cách giải

---

---

Với Các bài toán về các tập hợp số và cách giải sẽ giúp học sinh nắm vững lý thuyết, biết cách và phương pháp giải các dạng bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 10.

1. Lý thuyết:

- Tập hợp con của R : N ⊂ Z ⊂ Q ⊂ R  Trong đó:

N : là tập hợp số tự nhiên.

Z  : là tập hợp số nguyên.                                     

Q : là tập hợp số hữu tỷ.

R = ( -∞; +∞):  là tập hợp số thực.

- Các tập hợp con thường dùng của R 

 

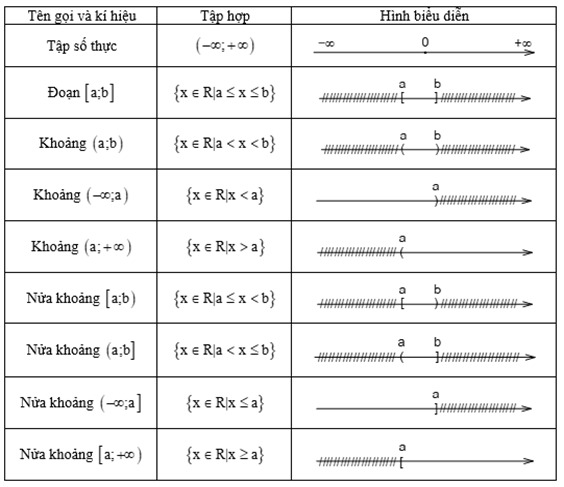
2. Phương pháp giải:

Sử dụng trục số, đoạn (hoặc khoảng) nào không lấy, ta gạch bỏ, sử dụng tính chất giao và hợp của các tập hợp để tìm ra kết quả.

3. Ví dụ minh họa:

Ví dụ 1: Xác định mỗi tập hợp sau và biểu diễn nó trên trục số.

a. (-3;3) ∪ ( -1;0) .

b. (-1;3) ∪ [0;5]  .

c. (-2;2] ∩ [1;3)  .

Lời giải:

Sử dụng trục số, đoạn (hoặc khoảng) nào không lấy, ta gạch bỏ, sử dụng tính chất giao và hợp của các tập hợp để tìm ra kết quả.

a. (-3;3) ∪ ( -1;0)  = (-3; 3).

 

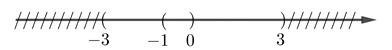
b. (-1;3) ∪ [0;5]  = (-1; 5].

c.  (-2;2] ∩ [1;3) = [1; 2]

 

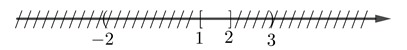
Ví dụ 2: Cho các tập hợp :

A = {x ∈ R | -3 ≤ x ≤ 2} .

B = {x ∈ R | 0 < x ≤ 7}.

C = {x ∈ R | x ≤ -1} .

D = {x ∈ R | x ≥ 5}.

Hãy dùng kí hiệu đoạn, khoảng, nửa khoảng để viết lại các tập hợp trên.

Lời giải:

 - Theo lý thuyết:[a;b] = {x ∈ R | a ≤ x ≤ b} .

Vậy A = {x ∈ R | -3 ≤ x ≤ 2} = [-3; 2].

- Theo lý thuyết: (a; b] = {x ∈ R | a < x ≤ b} .

Vậy  B = {x ∈ R | 0 < x ≤ 7} = (0; 7].

- Theo lý thuyết: (-∞; 1) = { x ∈ R | x < b } .

Vậy C = {x ∈ R | x < -1} = (-∞; 1).

- Theo lý thuyết: [a; +∞) = {x ∈ R | a ≤ x}  .

Vậy  D = {x ∈ R | x ≥ 5} = [5; +∞).

Ví dụ 3: Cho hai tập hợp A = {x ∈ R | -5 ≤ x < 1}; B = {x ∈ R | -3 < x ≤ 3}. Tìm A ∩ B

Lời giải:

Ta có: A = {x ∈ R | -5 ≤ x < 1} = [-5; 1) ( theo lý thuyết: [a; b) = {x ∈ R | -3 ≤ x < b} )

       B = {x ∈ R | -3 < x ≤ 3} = (-3; 3] ( theo lý thuyết: (a; b] = {x ∈ R | a < x ≤ b})

Ta biểu diễn tập hợp A và B trên trục số như sau:

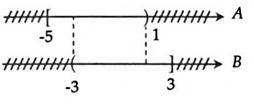
Vậy A ∩ B = (-3; 1).

4. Bài tập tự luyện:

Câu 1: Cho tập hợp A = {x ∈ R | -3 < x < 1} . Tập A là tập nào sau đây?

A.{-3; 1}.    

B. [-3; 1].    

C. [-3; 1).    

D. (-3; 1).

Lời giải:

Chọn D.

Theo lý thuyết: (a;b) = {x ∈ R | a < x < b} 

Vậy A = {x ∈ R | -3 < x < 1} = (-3; 1).

Câu 2: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1; 4]?

A.  

B.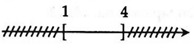    

C.    

D.     

Lời giải:

Chọn A. Vì (1; 4] gồm các số thực x mà 1 < x ≤ 4 .

Đáp án B sai vì [1; 4] gồm các số thực x mà 1 ≤ x ≤ 4 .

Đáp án C sai vì (1; 4) gồm các số thực x mà 1 < x < 4.

Đáp án B sai vì [1; 4) gồm các số thực x mà 1 ≤ x ≤ 4.

Câu 3: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A = { x ∈ R | 4 ≤ x ≤ 9} :

A. A = [4; 9].        

B. A = (4; 9].        

C. A = [4; 9).        

D. A = (4; 9)

Hướng dẫn: 

Chọn A. 

Theo lý thuyết: [a;b] = {x ∈ R | a ≤ x ≤ b} . Suy ra A = {x ∈ R | 4 ≤ x ≤ 9} = [4; 9] .

Câu 4: Cho hai tập hợp A = [-2; 7); B = (1; 9]. Tìm A ∪ B.

A. (1; 7).     

B. [-2; 9].    

C. [-2; 1).    

D. (7; 9].

Lời giải:

Chọn B.

Ta biểu diễn tập hợp A và B trên trục số như sau:

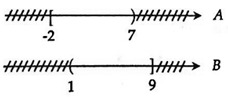
Vậy A ∪ B = [-2;7] ∪ (1;9] = [-2;9] .

Câu 5: Cho tập hợp X =  thì X được biểu diễn là hình nào sau đây?

A.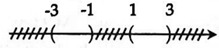   

B.    

C.    

D.    

Lời giải:

Chọn D.

Giải bất phương trình:

1 ≤ |x| ≤ 3 ⇔ ⇔ ⇔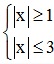  

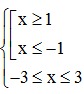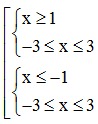
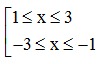⇔   ⇔ x ∈ [-3;-1] ∪ [1;3].

Vậy đáp án D thỏa mãn x ∈ [-3;-1] ∪ [1;3]  .

Câu 6: Cho hai tập hợp A = (1; 5]; B = (2; 7]. Tập hợp A \ B là:

A. (1; 2].     

B. (2; 5).     

C. (-1; 7].

D. (-1; 2).

Hướng dẫn: 

Chọn A.

Ta biểu diễn tập hợp A và B trên trục số:

 

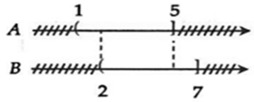
Vậy A \ B = { x ∈ R | x ∈ A và x ∉ B } ⇒ x ∈ (1; 2] .

Câu 7: Cho các số thực a, b, c, d và a < b < c < d. Khẳng định nào sau đây là đúng?

A. (a; c) ∩ (b; d) = (b; c)             

B. (a; c) ∩ (b; d) = (b; c] 

C. (a; c) ∩ (b; d) = [b; c)             

D. (a; c) ∪ (b; d) = [b; c)  

Lời giải:

Chọn A.

Ta biểu diễn (a; c); (b; d) trên trục số sau đó dựa vào tính chất giao của hai tập hợp để tìm ra đáp án:

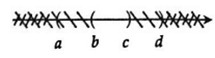
Vậy (a; c) ∩ (b; d) = (b; c).

Câu 8: Cho tập hợp A = [m; m+2]; B = [-1; 2]. Tìm điều kiện của m để A ⊂ B.

A. m ≤ -1 hoặc m ≥ 0 .   

B. -1  ≤ m ≤ 0 .       

C. -1  ≤ m ≤ 2  .

D. m < 1 hoặc m > 2.

Lời giải:

Chọn B.

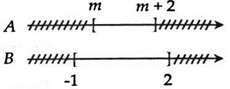
Điều kiện để A ⊂ B là: -1 ≤ m < m + 2 ≤ 2 ⇔ 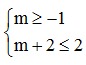⇔  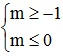⇔ -1  ≤ m ≤ 0   .

Câu 9: Cho hai tập hợp A = [-2; 3]; B = (m; m+6). Điều kiện để A ⊂ B là:

A. -3 ≤ m ≤ -2       

B. -3 < m < -2        

C. m < -3     

D. m ≥ -2  

Lời giải:

Chọn B.

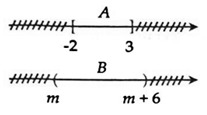
Điều kiện để A ⊂ B là m < -2 < 3 < m + 6 ⇔ 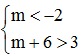⇔  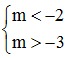⇔ -3 < m < 2  .

Câu 10: Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅ .

A.   .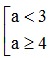

B. a < 3.

C. a < 0.      

D. a > 3.

Lời giải:

Chọn B.

 

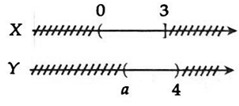
Xét: X ∩ Y ≠ ∅ ⇔ 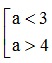⇔ 3 ≤ a ≤ 4

⇒ X ∩ Y ≠ ∅ ⇔ 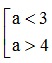. Mà theo đề bài, a ≤ 4 nên suy ra a < 3.

Vậy với a < 3 thì X ∩ Y ≠ ∅ .

Xem thêm các dạng bài tập Toán lớp 10 chọn lọc, có đáp án hay khác khác:

• Mệnh đề và suy luận toá học
• Các bài toán liên quan đến mệnh đề phủ định
• Tập hợp và cách xác định tập hợp
• Các phép toán trên tập hợp
• Các bài toán liên quan đến số gần đúng và sai số

Lời giải bài tập lớp 10 sách mới:

• Giải bài tập Lớp 10 Kết nối tri thức
• Giải bài tập Lớp 10 Chân trời sáng tạo
• Giải bài tập Lớp 10 Cánh diều

---

---

---