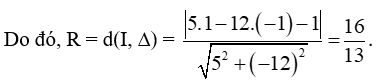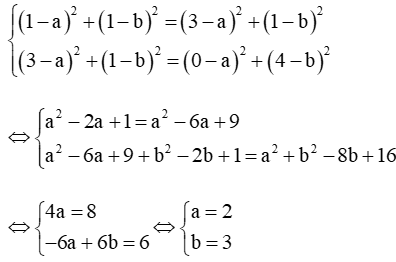Giải Toán 10 trang 91 Tập 2 Cánh diều
Với Giải Toán 10 trang 91 Tập 2 trong Bài 5: Phương trình đường tròn Toán 10 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 trang 91.
Bài 1 trang 91 Toán lớp 10 Tập 2: Phương trình nào sau đây là phương trình đường tròn?
a) x2 + y2 – 2x + 2y – 7 = 0;
b) x2 + y2 – 8x + 2y + 20 = 0.
Lời giải:
a) x2 + y2 – 2x + 2y – 7 = 0
⇔ (x2 – 2x + 1) + (y2 + 2y + 1) – 1 – 1 – 7 = 0
⇔ (x – 1)2 + (y + 1)2 = 9
Đây là phương trình đường tròn với tâm I(1; – 1) và bán kính R = = 3.
b) x2 + y2 – 8x + 2y + 20 = 0
⇔ (x2 – 8x + 16) + (y2 + 2y + 1) – 16 – 1 + 20 = 0
⇔ (x – 4)2 + (y – 1)2 = – 3
Do – 3 < 0 nên đây không phải là phương trình đường tròn.
Bài 2 trang 91 Toán lớp 10 Tập 2: Tìm tâm và bán kính của đường tròn trong mỗi trường hợp sau:
a) Đường tròn có phương trình (x + 1)2 + (y – 5)2 = 9;
b) Đường tròn có phương trình x2 + y2 – 6x – 2y – 15 = 0.
Lời giải:
a) Ta có: (x + 1)2 + (y – 5)2 = 9 ⇔ (x – (– 1))2 + (y – 5)2 = 32.
Do đó, đường tròn đã cho có tâm I(– 1; 5) và bán kính R = 3.
b) Ta có: x2 + y2 – 6x – 2y – 15 = 0
⇔ (x2 – 6x + 9) + (y2 – 2y + 1) – 9 – 1 – 15 = 0
⇔ (x – 3)2 + (y – 1)2 = 25
Do đó, đường tròn đã cho có tâm I(3; 1) và bán kính R = .
Bài 3 trang 91 Toán lớp 10 Tập 2: Lập phương trình đường tròn trong mỗi trường hợp sau:
a) Đường tròn có tâm O(– 3; 4) và bán kính R = 9;
b) Đường tròn có tâm I(5; – 2) và đi qua điểm M(4; – 1);
c) Đường tròn có tâm I(1; – 1) và có một tiếp tuyến là Δ: 5x – 12y – 1 = 0;
d) Đường tròn đường kính AB với A(3; – 4) và B(– 1; 6);
e) Đường tròn đi qua ba điểm A(1; 1); B(3; 1); C(0; 4).
Lời giải:
a) Phương trình đường tròn có tâm O(– 3; 4) và bán kính R = 9 là
(x – (– 3))2 + (y – 4)2 = 92 hay (x + 3)2 + (y – 4)2 = 81.
b) Đường tròn có tâm I và đi qua điểm M thì có bán kính là
R = IM = .
Vậy phương trình đường tròn cần lập là (x – 5)2 + (y – (– 2))2 = hay (x – 5)2 + ( y + 2)2 = 2.
c) Khoảng cách từ tâm I của đường tròn đến tiếp tuyến ∆ chính bằng bán kính của đường tròn.
Vậy phương trình đường tròn cần lập là hay .
d) Ta có: AB = .
Gọi I là trung điểm của AB, ta có tọa độ của I là hay I(1; 1).
Đường tròn đường kính AB có tâm là trung điểm I của AB và có bán kính R =
Vậy phương trình đường tròn đường kính AB là (x – 1)2 + (y – 1)2 = 29.
e) Giả sử tâm của đường tròn là điểm I(a; b).
Ta có IA = IB = IC ⇔ IA2 = IB2 = IC2.
Vì IA2 = IB2, IB2 = IC2 nên
Đường tròn tâm I(2; 3) bán kính R = IC = .
Phương trình đường tròn là .
Vậy phương trình đường tròn là (x – 2)2 + (y – 3)2 = 5.
Lời giải bài tập Toán 10 Bài 5: Phương trình đường tròn hay khác:
- Giải Toán 10 trang 87 Tập 2
- Giải Toán 10 trang 88 Tập 2
- Giải Toán 10 trang 89 Tập 2
- Giải Toán 10 trang 90 Tập 2
- Giải Toán 10 trang 92 Tập 2
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Cánh diều
- Giải Chuyên đề học tập Toán 10 Cánh diều
- Giải SBT Toán 10 Cánh diều
- Giải lớp 10 Cánh diều (các môn học)
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Soạn văn 10 (hay nhất) - Cánh diều
- Soạn văn 10 (ngắn nhất) - Cánh diều
- Soạn văn 10 (siêu ngắn) - Cánh diều
- Giải sgk Toán 10 - Cánh diều
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - Cánh diều
- Giải sgk Hóa học 10 - Cánh diều
- Giải sgk Sinh học 10 - Cánh diều
- Giải sgk Địa lí 10 - Cánh diều
- Giải sgk Lịch sử 10 - Cánh diều
- Giải sgk Kinh tế và Pháp luật 10 - Cánh diều
- Giải sgk Tin học 10 - Cánh diều
- Giải sgk Công nghệ 10 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 10 - Cánh diều
- Giải sgk Giáo dục quốc phòng 10 - Cánh diều