Giải Toán 10 trang 63 Tập 2 Cánh diều
Với Giải Toán 10 trang 63 Tập 2 trong Bài 1: Tọa độ của vectơ Toán 10 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 trang 63.
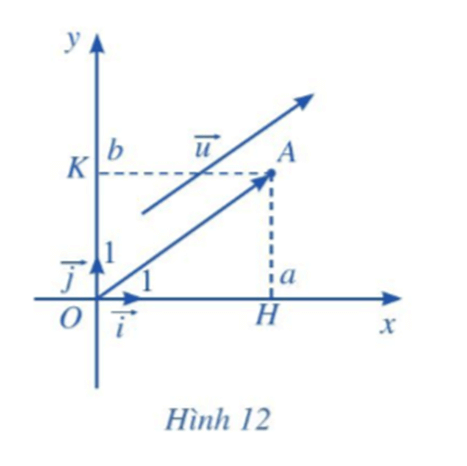
Hoạt động 4 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho vectơ . Ta chọn điểm A sao cho .
Xét vectơ đơn vị trên trục hoành Ox và vectơ đơn vị trên trục tung Oy (Hình 12).
a) Tìm hoành độ và tung độ của điểm A.
b) Biểu diễn vectơ qua vectơ .
c) Biểu diễn vectơ qua vectơ .
d) Chứng tỏ rằng .
Lời giải:
a) Ta có: , mà (a; b) là tọa độ của vectơ nên điểm A có hoành độ là a và tung độ là b.
b) Điểm H biểu diễn số a trên trục Ox nên .
c) Điểm K biểu diễn số b trên trục Oy nên .
d) Áp dụng quy tắc hình bình hành ta có: .
Mà , nên .
Theo bài ra ta có: .
Vậy .
Luyện tập 2 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho điểm B(– 1; 0) và vectơ = (0; – 7).
a) Biểu diễn vectơ qua hai vectơ và .
b) Biểu diễn vectơ qua hai vectơ và .
Lời giải:
a) Vì = (0; – 7) nên.
b) Vì điểm B có tọa độ là (– 1; 0) nên . Do đó:
.
Lời giải bài tập Toán 10 Bài 1: Tọa độ của vectơ hay khác:
- Giải Toán 10 trang 60 Tập 2
- Giải Toán 10 trang 61 Tập 2
- Giải Toán 10 trang 62 Tập 2
- Giải Toán 10 trang 64 Tập 2
- Giải Toán 10 trang 65 Tập 2
- Giải Toán 10 trang 66 Tập 2
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Cánh diều
- Giải Chuyên đề học tập Toán 10 Cánh diều
- Giải SBT Toán 10 Cánh diều
- Giải lớp 10 Cánh diều (các môn học)
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Soạn văn 10 (hay nhất) - Cánh diều
- Soạn văn 10 (ngắn nhất) - Cánh diều
- Soạn văn 10 (siêu ngắn) - Cánh diều
- Giải sgk Toán 10 - Cánh diều
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - Cánh diều
- Giải sgk Hóa học 10 - Cánh diều
- Giải sgk Sinh học 10 - Cánh diều
- Giải sgk Địa lí 10 - Cánh diều
- Giải sgk Lịch sử 10 - Cánh diều
- Giải sgk Kinh tế và Pháp luật 10 - Cánh diều
- Giải sgk Tin học 10 - Cánh diều
- Giải sgk Công nghệ 10 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 10 - Cánh diều
- Giải sgk Giáo dục quốc phòng 10 - Cánh diều