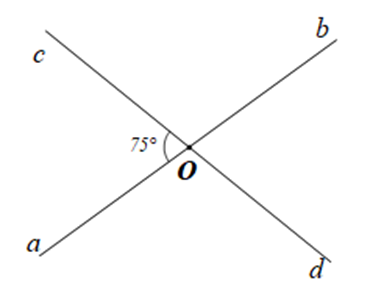
Cho các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau
Bài 2 trang 103 sách bài tập Toán lớp 7 Tập 1: Cho các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau. Tìm số đo mỗi góc aOc, bOc, bOd, aOd trong mỗi trường hợp sau:
a)
b)
c)
d)
e)
Lời giải:
Vì các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau nên ta có:
• và là hai góc đối đỉnh nên
• và là hai góc kề bù nên
• và là hai góc đối đỉnh nên .
a)
Vì (hai góc đối đỉnh) mà nên .
Vì (hai góc kề bù)
Suy ra .
Do đó .
Vậy và.
b) • Vì (hai góc đối đỉnh)
Mà
Nên hay
Suy ra
Do đó
• Vì (hai góc kề bù)
Suy ra .
Do đó .
Vậy và .
c) Vì nên ta có:
hay
Do đó
Mà nên
Hay do đó .
Vậy .
d) Vì nên
Mà
Do đó
Hay
Suy ra
Do đó
Khi đó
Suy ra và
Vậy và .
e) Vì và nên ta có:
hay
Suy ra
Khi đó
Suy ra và .
Vậy và .
Xem thêm các bài giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 7 hay khác:
- Giải sgk Toán 7 Cánh diều
- Giải SBT Toán 7 Cánh diều
- Giải lớp 7 Cánh diều (các môn học)
- Giải lớp 7 Kết nối tri thức (các môn học)
- Giải lớp 7 Chân trời sáng tạo (các môn học)
- Soạn văn 7 (hay nhất) - Cánh diều
- Soạn văn 7 (ngắn nhất) - Cánh diều
- Giải sgk Toán 7 - Cánh diều
- Giải Tiếng Anh 7 Global Success
- Giải Tiếng Anh 7 Friends plus
- Giải sgk Tiếng Anh 7 Smart World
- Giải Tiếng Anh 7 Explore English
- Giải sgk Khoa học tự nhiên 7 - Cánh diều
- Giải sgk Lịch Sử 7 - Cánh diều
- Giải sgk Địa Lí 7 - Cánh diều
- Giải sgk Giáo dục công dân 7 - Cánh diều
- Giải sgk Công nghệ 7 - Cánh diều
- Giải sgk Tin học 7 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 7 - Cánh diều
- Giải sgk Âm nhạc 7 - Cánh diều