Giải Toán 10 trang 99 Tập 2 Cánh diều

Trang trước Trang sau

Với Giải Toán 10 trang 99 Tập 2 trong Bài 6: Ba đường conic Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 99.

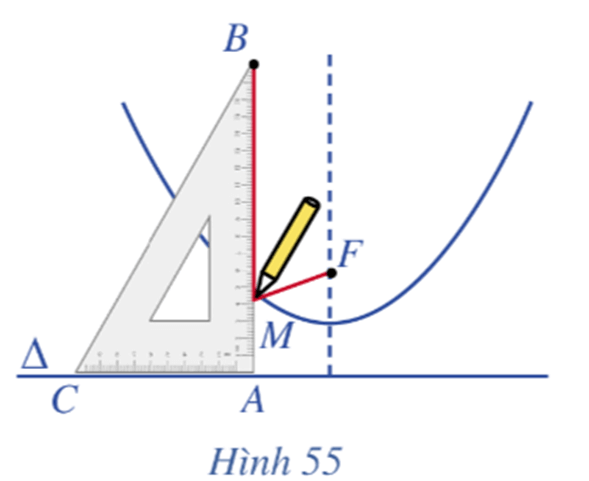
Hoạt động 5 trang 99 Toán lớp 10 Tập 2: Lấy đường thẳng ∆ và một điểm F không thuộc ∆. Lấy một ê ke ABC (vuông ở A) và một đoạn dây không đàn hồi, có độ dài bằng AB. Đính một đầu dây vào điểm F, đầu kia vào đỉnh B của ê ke. Đặt ê ke sao cho cạnh AC nằm trên ∆, lấy đầu bút chì (kí hiệu là điểm M) ép sát sợi dây vào cạnh AB và giữ căng sợi dây. Lúc này, sợi dây chính là đường gấp khúc BMF.

Cho cạnh AC của ê ke trượt trên ∆ (Hình 55). Khi đó, đầu bút chì M sẽ vạch nên một đường mà ta gọi là đường parabol.

Lấy đường thẳng denta và một điểm F không thuộc denta

Khi M thay đổi, có nhận xét gì về khoảng cách từ M đến F và khoảng cách từ M đến đường thẳng ∆?

Lời giải:

Khi M thay đổi, ta có: MA + MB = MF + MB (Vì các tổng này đều có độ dài bằng đoạn dây AB).

Do đó, MA = MF.

Mà MA vuông góc với ∆ tại A nên MA là khoảng cách từ M đến ∆.

Vậy khi M thay đổi khoảng cách từ M đến F luôn bằng khoảng cách từ M đến đường thẳng ∆.

Lời giải bài tập Toán lớp 10 Bài 6: Ba đường conic Cánh diều hay khác:

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Trang trước Trang sau
Giải bài tập lớp 10 Cánh diều khác