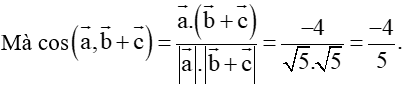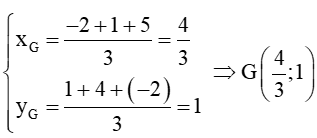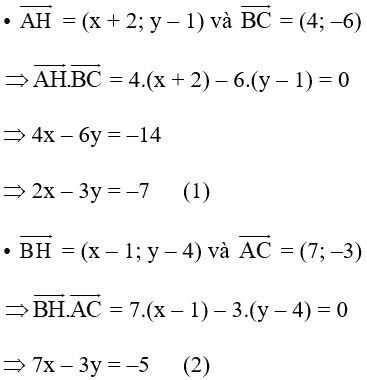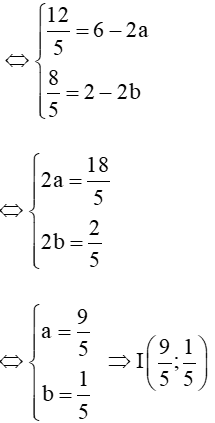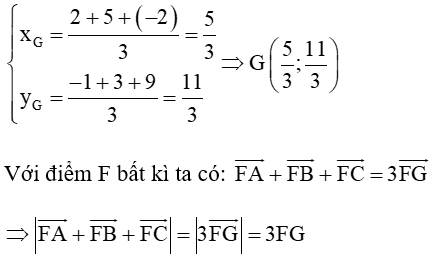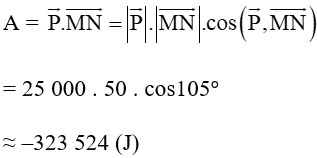Giải SBT Toán 10 trang 71 Tập 1 Kết nối tri thức
Với Giải SBT Toán 10 trang 71 Tập 1 trong Bài 11: Tích vô hướng của hai vectơ Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 71.
Bài 4.66 trang 71 sách bài tập Toán lớp 10 Tập 1: Cho bốn điểm A, B, C, D trong mặt phẳng. Chứng minh rằng
Lời giải:
Ta có:
•
•
•
Suy ra:
= 0.
Vậy
Bài 4.67 trang 71 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba vectơ = (1; 2), = (3; –4), = (–5; 3).
a) Tính các tích vô hướng
b) Tìm góc giữa hai vectơ và
Lời giải:
a) Với = (1; 2), = (3; –4) và = (–5; 3) ta có:
• = 1.3 + 2.(–4) = 3 – 8 = –5;
• = 3.(–5) + (–4).3 = –15 – 12 = –27;
• = (–5).1 + 3.2 = –5 + 6 = 1.
b) Với = (1; 2), = (3; –4) và = (–5; 3) ta có:
• = (–2; –1)
• = 1.(–2) + 2.(–1) = –2 – 2 = –4.
Vậy góc giữa hai vectơ và khoảng 143°7'48''.
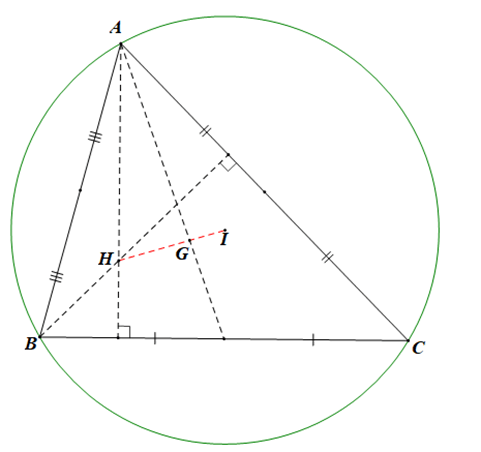
Bài 4.68 trang 71 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–2; 1), B(1; 4) và C(5; −2).
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tìm toạ độ trọng tâm G của tam giác ABC.
b) Tìm toạ độ trực tâm H và tâm đường tròn ngoại tiếp I của tam giác ABC.
Lời giải:
a) Với A(–2; 1), B(1; 4) và C(5; −2) ta có:
= (3; 3) và = (7; –3)
Vì nên hai vectơ và không cùng phương
Do đó ba điểm A, B, C không thẳng hàng
Vậy A, B, C là ba đỉnh của một tam giác.
Vì G là trọng tâm của tam giác ABC nên ta có:
Vậy tọa độ trọng tâm của tam giác ABC là: .
b) *Tìm tọa độ trực tâm H của tam giác ABC:
Vì H là trực tâm của tam giác ABC nên AH ⊥ BC và BH ⊥ AC
Hay và
Giả sử H(x; y) là tọa độ trực tâm tam giác ABC
Với A(–2; 1), B(1; 4), C(5; −2) và H(x; y) ta có:
Trừ vế theo vế (2) cho (1) ta có: 5x = 2
x =
Thay x = vào (1) ta được: 2. – 3y = –7
3y =
y =
Vậy tọa độ trực tâm của tam giác ABC là
* Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC:
Theo kết quả phần a) của Bài 4.15, trang 54, Sách Bài tập, Toán 10, tập một ta có:
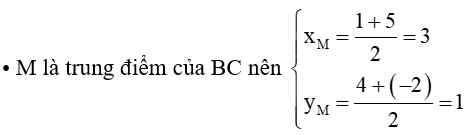
với M là trung điểm của BC.
Giả sử I(a; b) là tọa độ tâm đường tròn ngoại tiếp tam giác ABC
Với A(–2; 1), B(1; 4), C(5; −2), và I(a; b) ta có:
•
M(3; 1)
= (3 – a; 1 – b)
= (6 – 2a; 2 – 2b)
Ta có
Vậy tọa độ tâm đường tròn ngoại tiếp tam giác ABC là
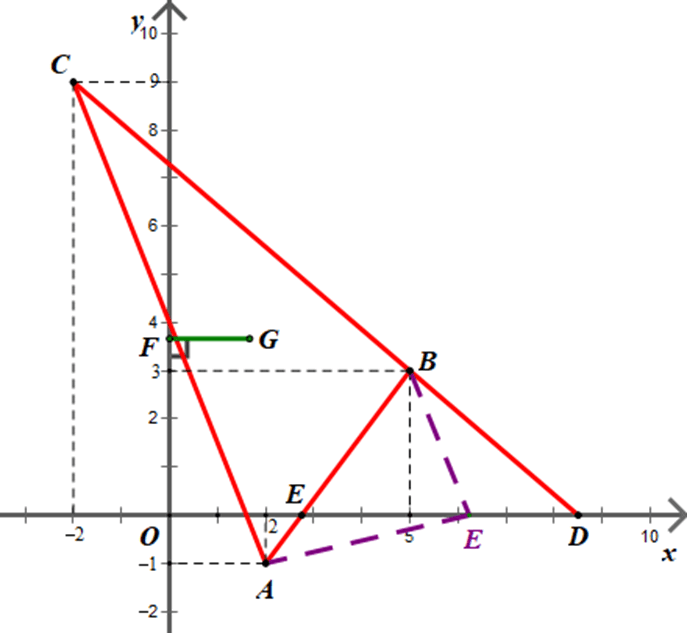
Bài 4.69 trang 71 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; −1), B(5; 3) và C(–2; 9).
a) Tìm điểm D thuộc trục hoành sao cho B, C, D thẳng hàng.
b) Tìm điểm E thuộc trục hoành sao cho EA + EB nhỏ nhất.
c) Tìm điểm F thuộc trục tung sao cho vectơ có độ dài ngắn nhất.
Lời giải:
a) Giả sử D(a; 0) là điểm thuộc trục hoành.
Với B(5; 3), C(–2; 9) và D(a; 0) ta có:
• = (–7; 6)
• = (a – 5; –3)
Vì ba điểm B, C, D thẳng hàng nên ta có: và là hai vectơ cùng phương
2(a – 5) = 7
a – 5 =
a =
Vậy là điểm cần tìm.
b) Ta có: A(2; −1), B(5; 3) là hai điểm nằm về hai phía của trục hoành
Do đó với mỗi điểm E nằm trên trục hoành ta luôn có EA + EB ≥ AB
Suy ra EA + EB ngắn nhất là bằng AB
Điều này xảy ra khi và chỉ khi E là giao điểm của AB và trục hoành Ox
3 điểm A, E, B thẳng hàng
và là hai vectơ cùng phương
Giả sử E(b; 0) là điểm thuộc trục hoành.
Với A(2; −1), B(5; 3) và E(b; 0) ta có:
• = (3; 4)
• = (b – 2; 1)
Khi đó và là hai vectơ cùng phương
b – 2 =
b =
Vậy là điểm cần tìm.
c) Gọi G là trọng tâm của tam giác ABC.
Khi đó với A(2; −1), B(5; 3) và C(–2; 9) ta có:
Để vectơ có độ dài ngắn nhất thì FG có độ dài ngắn nhất
Mà F là điểm nằm trên trục tung
Do đó F là hình chiếu vuông góc của G lên Oy.
Hoành độ của F là x = 0 và tung độ của F bằng với tung độ của G là y =
Vậy
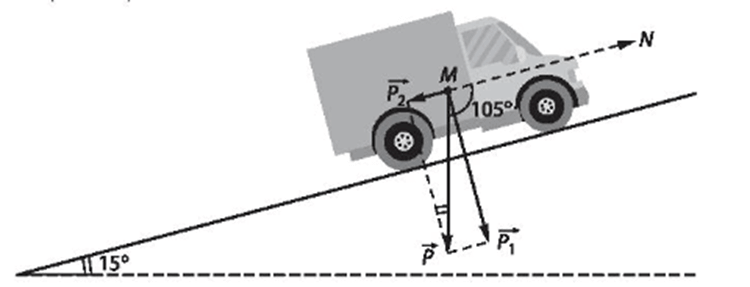
Bài 4.70 trang 71 sách bài tập Toán lớp 10 Tập 1: Một ô tô có khối lượng 2,5 tấn chạy từ chân lên đỉnh một con dốc thẳng. Tính công của trọng lực tác động lên xe, biết dốc dài 50 m và nghiêng 15° so với phương nằm ngang (trong tính toán, lấy gia tốc trọng trường bằng 10 m/s²).
Lời giải:
Đổi 2,5 tấn = 2 500 kg.
Trọng lực của ô tô hợp với hướng chuyển dời một góc là:
α = 90° + 15° = 105°.
Trọng lực được phân tích thành hai thành phần và nên ta có:
( có phương vuông góc với mặt dốc, có phương song song với mặt dốc)
Ta thấy không có tác dụng với chuyển dời của xe và ngược hướng với .
Do đó công của trọng lực tác động lên xe bằng:
Vậy công của trọng lực tác động lên xe bằng khoảng –323 524 J.
Lời giải sách bài tập Toán 10 Bài 11: Tích vô hướng của hai vectơ Kết nối tri thức hay khác:
- Giải SBT Toán 10 trang 66 Tập 1
- Giải SBT Toán 10 trang 67 Tập 1
- Giải SBT Toán 10 trang 68 Tập 1
- Giải SBT Toán 10 trang 69 Tập 1
- Giải SBT Toán 10 trang 70 Tập 1
Xem thêm lời Giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Kết nối tri thức
- Giải Chuyên đề học tập Toán 10 Kết nối tri thức
- Giải SBT Toán 10 Kết nối tri thức
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
- Soạn văn 10 (hay nhất) - KNTT
- Soạn văn 10 (ngắn nhất) - KNTT
- Soạn văn 10 (siêu ngắn) - KNTT
- Giải sgk Toán 10 - KNTT
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - KNTT
- Giải sgk Hóa học 10 - KNTT
- Giải sgk Sinh học 10 - KNTT
- Giải sgk Địa lí 10 - KNTT
- Giải sgk Lịch sử 10 - KNTT
- Giải sgk Kinh tế và Pháp luật 10 - KNTT
- Giải sgk Tin học 10 - KNTT
- Giải sgk Công nghệ 10 - KNTT
- Giải sgk Hoạt động trải nghiệm 10 - KNTT
- Giải sgk Giáo dục quốc phòng 10 - KNTT