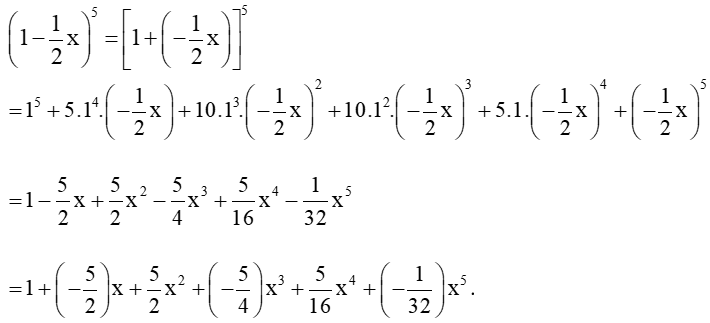Giải Toán 10 trang 19 Tập 2 Cánh diều

Với Giải Toán 10 trang 19 Tập 2 trong Bài 4: Nhị thức Newton Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 19.

Luyện tập 1 trang 19 Toán lớp 10 Tập 2: Khai triển biểu thức (2 + x)⁴.

Lời giải:

Ta có: (2 + x)⁴ = 2⁴ + 4 . 2³ . x + 6 . 2² . x² + 4 . 2 . x³ + x⁴

= 16 + 32x + 24x² + 8x³ + x⁴.

Luyện tập 2 trang 19 Toán lớp 10 Tập 2: Khai triển biểu thức (2 − 3y)⁴.

Lời giải:

Ta có: (2 – 3y)⁴ = [2 + (– 3y)]⁴

= 2⁴ + 4 . 2³ . (– 3y) + 6 . 2² . (– 3y)² + 4 . 2 . (– 3y)³ + (– 3y)⁴

= 16 – 96y + 216y² – 216y³ + 81y⁴.

Luyện tập 3 trang 19 Toán lớp 10 Tập 2: Tính:

a) $C_4^0+C_4^1+C_4^2+C_4^3+C_4^4$ ;

b) $C_5^0-C_5^1+C_5^2-C_5^3+C_5^4-C_5^5$ .

Lời giải:

a) $C_4^0+C_4^1+C_4^2+C_4^3+C_4^4$

= $=C_4^0.1^4+C_4^1.1^3.1+C_4^2{.1}^2{.1}^2+C_4^3{\mathrm{.1.1}}^3+C_4^4{.1}^4$

= (1 + 1)⁴

= 2⁴ = 16.

b) $C_5^0-C_5^1+C_5^2-C_5^3+C_5^4-C_5^5$

= $C_5^0{.1}^5+C_5^1{.1}^4.\left(-1\right)+C_5^2{.1}^3.{\left(-1\right)}^2+C_5^3{.1}^2.{\left(-1\right)}^3+C_5^4\mathrm{.1.}{\left(-1\right)}^4+C_5^5.{\left(-1\right)}^5$

= [1 + (– 1)]⁵

= 0⁵ = 0.

Bài 1 trang 19 Toán lớp 10 Tập 2: Khai triển các biểu thức sau:

a) (2x + 1)⁴;

b) (3y – 4)⁴;

c) ${\left(x+\frac{1}{2}\right)}^4$ ;

d) ${\left(x-\frac{1}{3}\right)}^4$ .

Lời giải:

a) (2x + 1)⁴ = (2x)⁴ + 4 . (2x)³ . 1 + 6 . (2x)² . 1² + 4 . (2x) . 1³ + 1⁴

= 16x⁴ + 32x³ + 24x² + 8x + 1.

b) (3y – 4)⁴ = [3y + (– 4)]⁴

= (3y)⁴ + 4 . (3y)³ . (– 4) + 6 . (3y)² . (– 4)² + 4 . (3y) . (– 4)³ + (– 4)⁴

= 81y⁴ – 432y³ + 864y² – 768y + 256.

c) ${\left(x+\frac{1}{2}\right)}^4=x^4+4.x^3.\frac{1}{2}+6.x^2.{\left(\frac{1}{2}\right)}^2+4.x.{\left(\frac{1}{2}\right)}^3+{\left(\frac{1}{2}\right)}^4$

$=x^4+2x^3+\frac{3}{2}{x}^2+\frac{1}{2}x+\frac{1}{16}$.

d) ${\left(x-\frac{1}{3}\right)}^4={\left(x+\left(-\frac{1}{3}\right)\right)}^4$

$=x^4+4.x^3.\left(-\frac{1}{3}\right)+6.x^2.{\left(-\frac{1}{3}\right)}^2+4.x.{\left(-\frac{1}{3}\right)}^3+{\left(-\frac{1}{3}\right)}^4$

$=x^4-\frac{4}{3}{x}^3+\frac{2}{3}{x}^2-\frac{4}{27}x+\frac{1}{81}$.

Bài 2 trang 19 Toán lớp 10 Tập 2: Khai triển các biểu thức sau:

a) (x + 1)⁵;

b) (x – 3y)⁵.

Lời giải:

a) (x + 1)⁵ = x⁵ + 5 . x⁴ . 1 + 10 . x³ . 1² + 10 . x² . 1³ + 5 . x . 1⁴ + 1⁵

= x⁵ + 5x⁴ + 10x³ + 10x² + 5x + 1.

b) (x – 3y)⁵ = [x + (– 3y)]⁵

= x⁵ + 5 . x⁴ . (– 3y) + 10 . x³ . (– 3y)² + 10 . x² . (– 3y)³ + 5 . x . (– 3y)⁴ + (– 3y)⁵

= x⁵ – 15x⁴y + 90x³y² – 270x²y³ + 405xy⁴ – 243y⁵.

Bài 3 trang 19 Toán lớp 10 Tập 2: Xác định hệ số của x⁴ trong khai triển biểu thức (3x + 2)⁵.

Lời giải:

Số hạng chứa x⁴ trong khai triển biểu thức (3x + 2)⁵ là $C_5^1.{\left(3x\right)}^4.2$ .

Ta có: $C_5^1.{\left(3x\right)}^4.2=\mathrm{5.81.2.}{x}^4=810x^4$ .

Vậy hệ số của x⁴ trong khai triển biểu thức (3x + 2)⁵ là 810.

Bài 4 trang 19 Toán lớp 10 Tập 2: Cho

${\left(1-\frac{1}{2}x\right)}^5=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+a_4{x}^4+a_5{x}^5$.

Tính:

a) a₃;

b) a₀ + a₁ + a₂ + a₃ + a₄ + a₅.

Lời giải:

Áp dụng nhị thức Newton ta có:

a) a₃ chính là hệ số của x³ trong khai triển biểu thức ${\left(1-\frac{1}{2}x\right)}^5$.

Do đó, $a_3=-\frac{5}{4}$ .

b) Tương tự câu a, ta có: $a_0=1,a_1=-\frac{5}{2},a_2=\frac{5}{2},a_4=\frac{5}{16},a_5=-\frac{1}{32}$.

Do đó, a₀ + a₁ + a₂ + a₃ + a₄ + a₅ = $1+\left(-\frac{5}{2}\right)+\frac{5}{2}+\left(-\frac{5}{4}\right)+\frac{5}{16}+\left(-\frac{1}{32}\right)$ .

Vậy a₀ + a₁ + a₂ + a₃ + a₄ + a₅ $=\frac{1}{32}$ .

Bài 5 trang 19 Toán lớp 10 Tập 2: Cho tập hợp A có 5 phần tử. Số tập hợp con của A là bao nhiêu?

Lời giải:

Mỗi cách trích ra một tập con gồm a phần tử trong 5 phần tử của A chính là một tổ hợp chập a của 5, hay số tập con gồm a phần tử của A là $C_5^a$ .

Số tập hợp con có 0 phần tử của A là $C_5^0$ .

Số tập hợp con có 1 phần tử của A là $C_5^1$ .

Số tập hợp con có 2 phần tử của A là $C_5^2$ .

Số tập hợp con có 3 phần tử của A là $C_5^3$ .

Số tập hợp con có 4 phần tử của A là $C_5^4$ .

Số tập hợp con có 5 phần tử của A là $C_5^5$ .

Do đó, số tập hợp con của A là: $C_5^0+C_5^1+C_5^2+C_5^3+C_5^4+C_5^5=32$ .

Vậy tập hợp A có 32 tập hợp con.

Lời giải bài tập Toán lớp 10 Bài 4: Nhị thức Newton Cánh diều hay khác:

• Giải Toán 10 trang 18 Tập 2

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

• Toán 10 Bài tập cuối chương 5 trang 20

• Toán 10 Bài 1: Số gần đúng. Sai số

• Toán 10 Bài 2: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm

• Toán 10 Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

• Toán 10 Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản

• Sổ lò xo Art of Nature Thiên Long màu xinh xỉu
• Biti's ra mẫu mới xinh lắm
• Tsubaki 199k/3 chai
• L'Oreal mua 1 tặng 3

---