Giải SBT Toán 7 trang 115 Tập 1 Cánh diều
Với Giải Sách bài tập Toán 7 trang 115 Tập 1 trong Bài tập cuối chương 4 SBT Toán 7 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 115.
Bài 34 trang 115 sách bài tập Toán lớp 7 Tập 1:
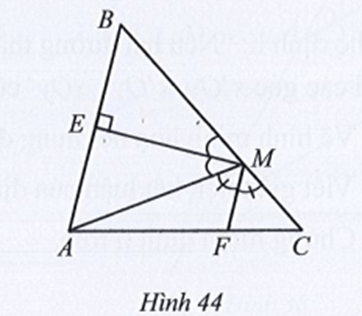
Quan sát Hình 44, biết ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của góc AMB và AMC. Vì sao hai đường thẳng MF và AB song song với nhau?
Lời giải:
Vì ME, MF lần lượt là tia phân giác của góc AMB và AMC nên:
và
Mặt khác và là hai góc kề bù nên ta có:
Lại có và là hai góc kề nhau nên:
Do đó
Hay
Suy ra (cùng bằng 90°).
Mà và là hai góc so le trong nên MF // AB.
Vậy MF và AB song song với nhau.
Bài 35 trang 115 sách bài tập Toán lớp 7 Tập 1:
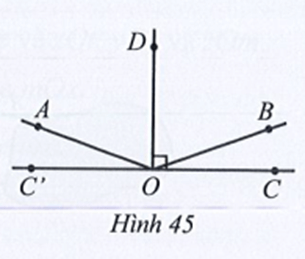
Quan sát Hình 45. Cho OD vuông góc với CC’ tại O,
a) Tính số đo mỗi góc AOB, BOC.
b) Tia OD có là tia phân giác của góc AOB hay không?
c) So sánh hai góc AOC và BOC’.
Lời giải:
a) Vì và là hai góc kề nhau nên ta có:
Mà
Nên và
Vậy và
b) Vì OD ⊥ CC’ tại O nên
Do hai góc BOC và BOD là hai góc kề nhau nên:
Suy ra
Do hai góc AOD và COD là hai góc kề nhau nên:
Suy ra
Do đó (cùng bằng 70°).
Mặt khác tia OD nằm giữa hai tia OA và OB nên tia OD là tia phân giác của góc AOB.
Vậy tia OD là tia phân giác của góc AOB.
c) Ta có (hai góc kề bù)
Suy ra
Do đó (cùng bằng 160°).
Vậy
Bài 36 trang 115 sách bài tập Toán lớp 7 Tập 1:
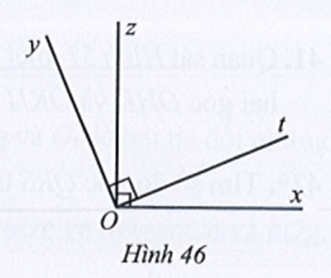
Quan sát Hình 46, biết Ox vuông góc với Oz và Oy vuông góc với Ot.
a) Hai góc xOt và yOz có bằng nhau hay không?
b) Chứng tỏ
c) Vẽ tia Ou là tia phân giác của góc tOz. Tia Ou có phải là tia phân giác của góc xOy hay không?
Lời giải:
a) Do hai góc xOt và tOz là hai góc kề nhau nên ta có:
(Ox ⊥ Oz).
Suy ra (1)
Do hai góc yOz và tOz là hai góc kề nhau nên ta có:
(Oy ⊥ Ot).
Suy ra (2)
Từ (1) và (2) ta có
Vậy
b) Ta có hai góc xOz và yOz là hai góc kề nhau nên ta có:
Khi đó
= 90° + 90° = 180°.
Vậy
c)
Do hai góc xOt và tOu là hai góc kề nhau nên ta có:
Do hai góc uOz và yOz là hai góc kề nhau nên ta có:
Mà Ou là tia phân giác của nên .
(theo phần a).
Suy ra
Mặt khác tia Ou nằm giữa hai tia Ox và Oy nên Ou có phải là tia phân giác của góc xOy.
Vậy Ou có phải là tia phân giác của góc xOy.
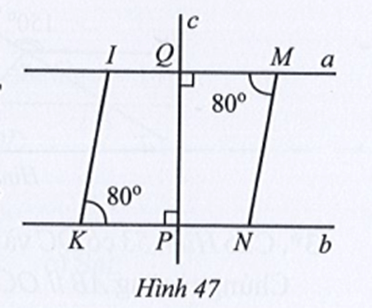
Bài 37 trang 115 sách bài tập Toán lớp 7 Tập 1: Quan sát Hình 47.
a) Vì sao hai đường thẳng a và b song song với nhau?
b) Tìm số đo góc MIK.
c) Vì sao hai đường thẳng MN và IK song song với nhau?
Lời giải:
a) Ta có (cùng bằng 90°).
Mà hai góc MQP và QPN là hai góc ở vị trí so le trong nên a // b.
Vậy a // b.
b) Vì a // b (theo phần a) nên
Suy ra
Vậy
c) Do hai góc IMN và aMN là hai góc kề bù nên ta có:
Suy ra
Do đó (cùng bằng 100°).
Mà hai góc MIN và aMN ở vị trí đồng vị nên MN // IK.
Vậy MN // IK.
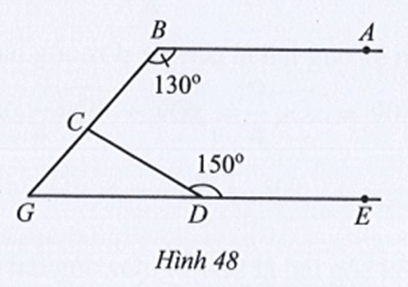
Bài 38 trang 115 sách bài tập Toán lớp 7 Tập 1: Tìm số đo góc BCD trong Hình 48, biết AB // DE.
Lời giải:
Kẻ Cx // AB (hình vẽ).
Do Cx // AB nên (hai góc trong cùng phía).
Suy ra
Do AB // DE nên (hai góc trong cùng phía)
Suy ra
Khi đó (cùng bằng 50°).
Mà hai góc BCx và BGE ở vị trí đồng vị nên Cx // GE.
Suy ra (hai góc trong cùng phía)
Do đó
Ta có hai góc BCx và xCD là hai góc kề nhau nên:
Vậy
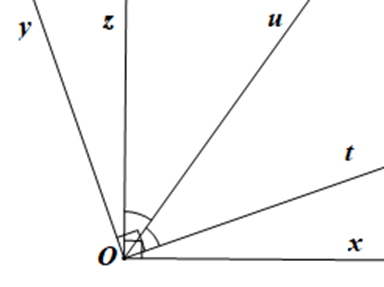
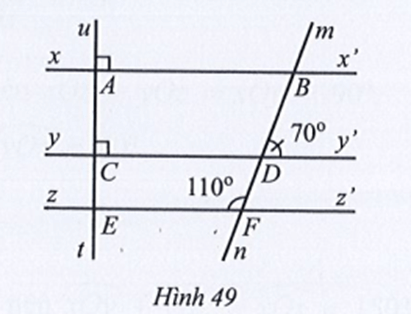
Bài 39 trang 115 sách bài tập Toán lớp 7 Tập 1: Quan sát Hình 49.
Chứng tỏ:
a) yy’ // zz’;
b) ut ⊥ zz’;
c) xx’ // zz’.
Lời giải:
a) Ta có (hai góc kề bù)
Suy ra
Do đó (cùng bằng 70°).
Mà và ở vị trí đồng vị nên yy’ // zz’.
Vậy yy’ // zz’.
b) Vì yy’ // zz’ (theo phần a) nên ta có:
(hai góc đồng vị).
Do đó ut ⊥ zz’.
Vậy ut ⊥ zz’.
c) Ta có (cùng bằng 90°).
Mà và ở vị trí đồng vị nên xx’ // zz’.
Vậy xx’ // zz’.
Lời giải sách bài tập Toán 7 Bài tập cuối chương 4 Cánh diều hay khác:
Xem thêm lời Giải sách bài tập Toán 7 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 7 hay khác:
- Giải sgk Toán 7 Cánh diều
- Giải SBT Toán 7 Cánh diều
- Giải lớp 7 Cánh diều (các môn học)
- Giải lớp 7 Kết nối tri thức (các môn học)
- Giải lớp 7 Chân trời sáng tạo (các môn học)
- Soạn văn 7 (hay nhất) - Cánh diều
- Soạn văn 7 (ngắn nhất) - Cánh diều
- Giải sgk Toán 7 - Cánh diều
- Giải Tiếng Anh 7 Global Success
- Giải Tiếng Anh 7 Friends plus
- Giải sgk Tiếng Anh 7 Smart World
- Giải Tiếng Anh 7 Explore English
- Giải sgk Khoa học tự nhiên 7 - Cánh diều
- Giải sgk Lịch Sử 7 - Cánh diều
- Giải sgk Địa Lí 7 - Cánh diều
- Giải sgk Giáo dục công dân 7 - Cánh diều
- Giải sgk Công nghệ 7 - Cánh diều
- Giải sgk Tin học 7 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 7 - Cánh diều
- Giải sgk Âm nhạc 7 - Cánh diều