Giải SBT Toán 10 trang 43 Tập 1 Kết nối tri thức
Với Giải SBT Toán 10 trang 43 Tập 1 trong Bài tập cuối chương 3 trang 40, 41, 42, 43, 44 Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 43.
Bài 3.36 trang 43 sách bài tập Toán lớp 10 Tập 1: Một ca nô xuất phát từ cảng A, chạy theo hướng đông với vận tốc 60 km/h. Cùng lúc đó, một tàu cá, xuất phát từ A, chạy theo hướng N30°E với vận tốc 50 km/h. Sau 2 giờ, hai tàu cách nhau bao nhiêu kilômét?
A. 110 km;
B. 112 km;
C. 111,4 km;
D. 110,5 km.
Lời giải:
Đáp án đúng là: C
Giả sử chuyển vị trí của cảng A, ca nô và tàu cá sau 2 giờ chuyển động được mô tả như hình vẽ sau:
Vì ca nô chuyển động theo hướng đông và tàu cá chuyển động theo hướng N30°E nên ta có:
Sau 2 giờ ca nô chạy được quãng đường AB bằng:
2.60 = 120 (km)
Sau 2 giờ tàu cá chạy được quãng đường AC bằng:
2.50 = 100 (km)
Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos
BC2 = 1202 + 1002 – 2.120.100.cos60°
BC2 = 12 400
BC ≈ 111,4 (km).
Ta chọn phương án C.
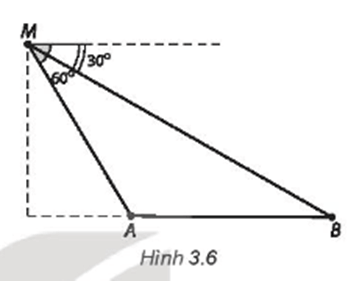
Bài 3.37 trang 43 sách bài tập Toán lớp 10 Tập 1: Một người đứng trên đài quan sát đặt ở cuối một đường đua thẳng. Ở độ cao 6 m so với mặt đường đua, tại một thời điểm người đó nhìn hai vận động viên A và B dưới các góc tương ứng là 60° và 30°, so với phương nằm ngang (H.3.6).
Khoảng cách giữa hai vận động viên A và B (làm tròn đến hàng đơn vị, theo đơn vị mét) tại thời điểm đó là
A. 8 m.
B. 7 m.
C. 6 m.
D. 9 m.
Lời giải:
Đáp án đúng là: B
Gọi H là chân đài quan sát ở cuối đường đua.
Khi đó ta có:
• MH = 6 (m);
•
•
Tam giác AMH vuông tại H nên ta có:
HA = MH.tan = 6.tan30° =
Tam giác BMH vuông tại H nên ta có:
HB = MH.tan = 6.tan60°
Do đó AB = HB – HA = ≈ 7 (m).
Ta chọn phương án B.
Bài 3.38 trang 43 sách bài tập Toán lớp 10 Tập 1: Cho góc tù α có sinα =
a) Tính cosα, tanα, cotα.
b) Tính giá trị của các biểu thức:
A = sinα. cot(180° – α) + cos(180° – α).cot(90° – α);
Lời giải:
a) Vì α là góc tù (90° < α < 180°) nên cosα < 0.
Ta có sin2α + cos2α = 1
+ cos2α = 1
cos2α =
cosα = (do cosα < 0)
Do đó:
• tanα
• cotα =
Vậy cosα = tanα = và cotα =
b) Ta có:
• cot(180° – α) = –cotα;
• cos(180° – α) = –cosα;
• cot(90° – α) = tanα;
Khi đó:
A = sinα. cot(180° – α) + cos(180° – α).cot(90° – α)
= sinα.(–cotα) + (–cosα).tanα
Vậy và B = –3.
Bài 3.39 trang 43 sách bài tập Toán lớp 10 Tập 1: Cho sin15° =
a) Tính sin75°, cos105°, tan165°.
b) Tính giá trị của biểu thức:
A = sin75°. cos165° + cos105°. sin165°.
Lời giải:
Vì 0° < 15° < 90° nên cos15° > 0.
Ta có sin215° + cos215° = 1
+ cos215° = 1
cos215° =
cos15° =
cos15°
Do đó:
tan15° =
a) Ta có:
• sin75° = sin(90° – 15°) = cos15° =
• cos105° = cos(180° – 75°) = –cos75°
= –cos(90° – 15°) = –sin15°
Þ cos105° =
• tan165° = tan(180° – 15°) = –tan15°
tan165° =
Vậy sin75° = cos105° = và tan165° =
b) Ta có:
• sin165° = sin(180° – 15°) = sin15°
sin165° =
• cos165° = cos(180° – 15°) = –cos15°
cos165° =
Khi đó:
A = sin75°. cos165° + cos105°. sin165°
=
Vậy A = –1.
Bài 3.40 trang 43 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 1, BC = 2 và Tính độ dài cạnh và số đo các góc còn lại của tam giác.
Lời giải:
Cách 1:
Áp dụng định lí côsin cho tam giác ABC ta có:
AC2 = AB2 + BC2 – 2.AB.BC.cos
AC2 = 12 + 22 – 2.1.2.cos60°
AC2 = 3
AC =
Áp dụng định lí sin cho tam giác ABC ta có:
và
và
Vậy và
Cách 2:
Tam giác ABC có AB = 1, BC = 2 nên
Mà
Do đó tam giác ABC vuông tại A
Suy ra
Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:
AC2 = BC2 – AB2 = 22 – 12 = 3
AC =
Vậy và
Lời giải sách bài tập Toán 10 Bài tập cuối chương 3 trang 40, 41, 42, 43, 44 Kết nối tri thức hay khác:
- Giải SBT Toán 10 trang 40 Tập 1
- Giải SBT Toán 10 trang 41 Tập 1
- Giải SBT Toán 10 trang 42 Tập 1
- Giải SBT Toán 10 trang 44 Tập 1
Xem thêm lời Giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Kết nối tri thức
- Giải Chuyên đề học tập Toán 10 Kết nối tri thức
- Giải SBT Toán 10 Kết nối tri thức
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
- Soạn văn 10 (hay nhất) - KNTT
- Soạn văn 10 (ngắn nhất) - KNTT
- Soạn văn 10 (siêu ngắn) - KNTT
- Giải sgk Toán 10 - KNTT
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - KNTT
- Giải sgk Hóa học 10 - KNTT
- Giải sgk Sinh học 10 - KNTT
- Giải sgk Địa lí 10 - KNTT
- Giải sgk Lịch sử 10 - KNTT
- Giải sgk Kinh tế và Pháp luật 10 - KNTT
- Giải sgk Tin học 10 - KNTT
- Giải sgk Công nghệ 10 - KNTT
- Giải sgk Hoạt động trải nghiệm 10 - KNTT
- Giải sgk Giáo dục quốc phòng 10 - KNTT