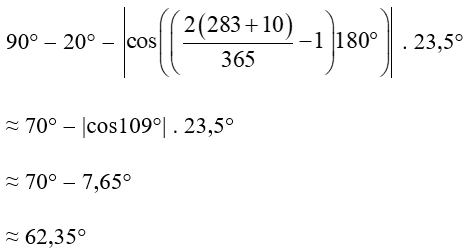Giải SBT Toán 10 trang 33 Tập 1 Kết nối tri thức
Với Giải SBT Toán 10 trang 33 Tập 1 trong Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 33.
Bài 3.3 trang 33 sách bài tập Toán lớp 10 Tập 1: Cho góc α thỏa mãn 0° < α < 180°, tanα = 2. Tính giá trị của các biểu thức sau:
a) G = 2sin α + cos α;
b) H = .
Lời giải:
Do 0° < α < 180° nên sinα > 0.
Mà tanα = = 2 > 0 nên sin α và cos α cùng dấu, do đó cosα > 0.
Do tanα = = 2 nên sinα = 2cosα
sin2α = 4cos2α
Ta có sin2α + cos2α = 1
4cos α + cos2α = 1
5cos2α = 1
cos2α =
Do cosα > 0 nên cosα = .
Do đó sinα = .
a) G = 2sinα + cosα
= 2 . +
=
= =
Vậy G = .
b) H =
= =
= = 5
Vậy H = 5.
Bài 3.4 trang 33 sách bài tập Toán lớp 10 Tập 1: Cho góc α thỏa mãn 0° < α < 180°, tanα = . Tính giá trị của biểu thức
K = .
Lời giải:
Do 0° < α < 180° nên sinα > 0.
Mà tanα = = > 0 nên sinα và cosα cùng dấu, do đó cosα > 0.
Chia cả tử và mẫu của K cho cos3α ta được:
K =
=
=
=
=
=
=
= =
= =
=
Vậy K = 2 +
Bài 3.5 trang 33 sách bài tập Toán lớp 10 Tập 1: Chứng minh rằng:
a) sin4α + cos4α = 1 - 2sin2α . cos2α;
b) sin6α + cos6α = 1 - 3sin2α . cos2α;
c*) .
Lời giải:
a) Ta có (sin2α + cos2α)2 = sin4α + 2sin2α . cos2α + cos4α
12 = sin4α + cos4α + 2sin2α . cos2α
sin4α + cos4α = 1 - 2sin2α . cos2α
Vậy sin4α + cos4α = 1 - 2sin2α . cos2α.
b) Ta có (sin2α + cos2α)3 = sin6α + cos6α + 3sin2α . cos2α(sin2α + cos2α)
13 = sin6α + cos6α + 3sin2α . cos2α . 1
sin6α + cos6α = 1 - 3sin2α . cos2α
Vậy sin6α + cos6α = 1 - 3sin2α . cos2α.
c) Xét sin4α + 6cos2α + 3
= sin4α + 6(1 - sin2α) + 3
= sin4α - 6sin2α + 9
= (sin2α - 3)2
= |sin2α – 3| = 3 - sin2α
(do 0 ≤ sin2α < 1 nên sin2α – 3 < 0).
Xét cos4α + 4sin2α
= cos4α + 4(1 - cos2α)
= cos4α - 4 cos2α + 4
= (cos2α - 2)2
= |cos2α – 2| = 2 - cos2α
(do 0 ≤ cos2α < 1 nên cos2α – 2 < 0).
= 3 - sin2 α + 2 - cos2 α
= 5 - (sin2 α + cos2 α)
= 5 - 1
= 4.
Vậy .
Bài 3.6 trang 33 sách bài tập Toán lớp 10 Tập 1: Góc nghiêng của Mặt Trời tại một vị trí trên Trái Đất là góc nghiêng giữa tia nắng lúc giữa trưa với mặt đất. Trong thực tế, để đo trực tiếp góc này, vào giữa trưa (khoảng 12 giờ), em có thể dựng một thước thẳng vuông góc với mặt đất, đo độ dài của bóng thước trên mặt đất. Khi đó, tang của góc nghiêng Mặt Trời tại vị trí đặt thước bằng tỉ số giữa độ dài của thước và độ dài của bóng thước. Góc nghiêng của Mặt Trời phụ thuộc vào vĩ độ của vị trí đo và phụ thuộc vào thời gian đo trong năm (ngày thứ mấy trong năm). Tại vị trí có vĩ độ và ngày thứ N trong năm, góc nghiêng của Mặt Trời α còn được tính theo công thức sau:
trong đó m = 0 nếu 1 ≤ N ≤ 172, m = 1 nếu 173 ≤ N ≤ 355, m = 2 nếu 356 ≤ N ≤ 365.
a) Hãy áp dụng công thức trên để tính góc nghiêng của Mặt Trời vào ngày 10/10 trong năm không nhuận (năm mà tháng 2 có 28 ngày) tại vị trí có vĩ độ = 20°.
b) Hãy xác định vĩ độ tại nơi em sinh sống và tính góc nghiêng của Mặt Trời tại đó theo hai cách đã được đề cập trong bài toán (đo trực tiếp và tính theo công thức) và so sánh hai kết quả thu được.
Lời giải:
Tháng 10 và tháng 12 có 31 ngày; tháng 11 có 30 ngày.
Nên từ 10/10 đến hết tháng 10 còn 21 ngày.
Do đó ngày 10/10 trong năm không nhuận là ngày thứ: 365 - 21 - 30 - 31 = 283 trong năm đó.
Vì 173 ≤ N = 283 ≤ 355 nên m = 1.
Góc nghiêng của Mặt Trời vào ngày 10/10 tại vị trí có vĩ độ = 20° là:
Vậy góc nghiêng của Mặt Trời vào ngày 10/10 tại vị trí có vĩ độ = 20° khoảng 62,35°.
b) Học sinh tự thực hiện việc đo và tính theo công thức để so sánh.
Lưu ý tại vị trí có vĩ độ f và ngày thứ N trong năm, góc nghiêng của Mặt Trời α còn được tính theo công thức sau:
trong đó m = 0 nếu 1 ≤ N ≤ 172, m = 1 nếu 173 ≤ N ≤ 355, m = 2 nếu 356 ≤ N ≤ 365.
Lời giải sách bài tập Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ Kết nối tri thức hay khác:
Xem thêm lời Giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Kết nối tri thức
- Giải Chuyên đề học tập Toán 10 Kết nối tri thức
- Giải SBT Toán 10 Kết nối tri thức
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
- Soạn văn 10 (hay nhất) - KNTT
- Soạn văn 10 (ngắn nhất) - KNTT
- Soạn văn 10 (siêu ngắn) - KNTT
- Giải sgk Toán 10 - KNTT
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - KNTT
- Giải sgk Hóa học 10 - KNTT
- Giải sgk Sinh học 10 - KNTT
- Giải sgk Địa lí 10 - KNTT
- Giải sgk Lịch sử 10 - KNTT
- Giải sgk Kinh tế và Pháp luật 10 - KNTT
- Giải sgk Tin học 10 - KNTT
- Giải sgk Công nghệ 10 - KNTT
- Giải sgk Hoạt động trải nghiệm 10 - KNTT
- Giải sgk Giáo dục quốc phòng 10 - KNTT